Камера на 200 мегапикселей от Samsung. Достигнут ли предел?

Поводом для написания этой статьи, помимо, собственно, появления первых 200-Мп мобильных матриц от Samsung, стали многочисленные обсуждения новостей, связанных с этим событием.

Зачастую в комментариях, написанных в саркастическом тоне, можно увидеть одни и те же повторяемые из года в год тезисы, отличающиеся только количеством обсуждаемых мегапикселей:

• Какие еще 200 мегапикселей?! Профессиональные дорогущие сменные объективы для зеркальных камер не способны разрешить такую матрицу, а мы говорим о каком-то «дверном глазке», сделанном из пластмассы! О какой резкости может вообще идти речь?
• Пиксели уже стали меньше длины волны света, соответственно, в такие пиксели просто «не влезет» нужный нам цвет!
• Всё это маркетинговая ерунда, так как «реальных пикселей» здесь не 200 млн, а всего 12! Ведь все пиксели в такой матрице группируются по 16 штук под одним цветным фильтром. Да и сигнал считывается не с каждого пикселя, а только группами!
• Даже природа ставит крест на подобных матрицах, уничтожая дифракцией саму идею сверхвысокого разрешения!

Что ж, возражения действительно интересные и многие из них вполне разумные. Тем не менее, тема мобильных объективов и мегапикселей окутана огромным количеством мифов и заблуждений.

Поэтому предлагаю детально обсудить вопрос разрешения камер современных смартфонов, пользуясь простым и понятным языком.

Действительно ли вам нужна матрица на 200 Мп для печати на билбордах?

Несмотря на то, что первый 200-Мп сенсор ISOCELL HP1 был представлен еще в сентябре прошлого года, он так и не появился ни в одном смартфоне.

Но Samsung уже показала продолжение линейки своих 200-мегапиксельных сенсоров в рекламе нового ISOCELL HP3. Суть этой рекламы сводится к тому, что снимки с нового мобильного сенсора теперь можно печатать даже на гигантских билбордах!

Вот сам ролик:

Кстати, если вы внимательно смотрели рекламу, то могли заметить, что на 24-й секунде к мобильной матрице ISOCELL HP3 через адаптер подключили огромный объектив от профессиональной камеры.

Этот момент смутил многих зрителей, хотя в действительности итоговый снимок, который был распечатан на билборде и показан в рекламе, компания сделала именно на крохотный мобильный объектив, без использования крупных линз.

Впрочем, это не так важно, и дальше вы поймете, почему.

Так причем здесь мегапиксели и билборд?

Упомянутая реклама явно рассчитана на людей, не имеющих никакого представления о билбордах, четкости изображения и физиологии зрения.

Неосведомленному зрителю может показаться невероятным тот факт, что снимки со смартфона уже можно распечатывать на площади в несколько сотен квадратных метров и всё это будет выглядеть вполне прилично.

На самом же деле, высокое разрешение не имеет никакого отношения к билбордам. И существует большое количество превосходно выглядящих рекламных щитов, снимки для которых сделаны на «старенький» iPhone:

Чтобы лучше понять это, давайте представим фотографию формата А4 (обычный офисный листок бумаги 21×30 см). Это сравнительно большой снимок. Каким же разрешением должна обладать камера, чтобы вы не смогли разглядеть отдельных пикселей на итоговом снимке?

Ответ на этот вопрос зависит от того, с какого расстояния вы будете смотреть на снимок.

Несколько слов о PPI

Все мы понимаем, что чем выше плотность пикселей, то есть, чем больше пикселей (точек, из которых состоит изображение) помещается в один дюйм или миллиметр, тем выше качество. Измеряется этот показатель в ppi (от англ. pixels per inch — пикселей на дюйм).

Если, к примеру, плотность пикселей составляет 300 ppi, то это означает, что в одном дюйме или в 25,4 мм помещается 300 точек изображения. Соответственно, если мы разделим 1 дюйм на значение ppi, то узнаем размер одного пикселя: 25.4 мм / 300 ppi = 0,08 мм или 80 микрометров (мкм).

Теперь возвращаемся к вопросу о снимке формата А4. Какая же плотность пикселей нужна для идеальной детализации? Основываясь на физиологии нашего зрения, я могу предложить очень простую формулу, которая подходит для человека с хорошим зрением:

Плотность пикселей = 10500 / расстояние до изображения в (см)

То есть, нужно просто разделить число 10500 на расстояние в сантиметрах, с которого вы будете смотреть на снимок. Если мы будем всматриваться в листок А4 с расстояния в 30 см, тогда в идеале плотность пикселей должна составлять 350 ppi (10500/30 см).

Конечно, при печати нужно учитывать и детализацию самого принтера, то есть, какое максимальное количество капель он способен нанести на один дюйм бумаги (dpi). Но в рамках нашего разговора это не так важно.

Если для снимка А4, который мы будем рассматривать прямо перед глазами, нужно 350 ppi, тогда разрешение такого снимка в идеале должно составлять 12 Мп. Это число вычисляется очень просто:

• Размер листа А4 в дюймах: 11.7″ на 8.3″
• Размер в пикселях: 11.7 * 350 на 8.3 * 350
• Получаем изображение 4095 на 2905 пикселей
• Это равно 4095 * 2905 = 11.9 млн пикселей или ~12 Мп

А теперь самое интересное!

Представим, что на этот же снимок мы будем смотреть уже с расстояния в 1 метр. То есть, пусть это будет фотография формата А4, висящая на стене в ста сантиметрах от зрителя.

Какое теперь будет требование к детализации? Считаем: 10500/100 = ~105 ppi! Пересчитываем это на мегапиксели и получаем цифру: 1 Мп (1228 x 871)! Мы увеличили расстояние до снимка всего в ~3.3 раза (было 30 см, стало 100 см), а требование к общему разрешению упало в 12 раз!

Даже если мы заменим А4 на более крупный формат — А1 (60 на 84 см), требование к снимку составит всего 8.5 Мп!

А если мы продолжим делать расчеты, то осознаем одну простую вещь: на большинстве огромных билбордов распечатаны снимки, разрешение которых не превышает 12 Мп! То есть, разрешения камеры того же iPhone вполне достаточно.

Использовать более высокое разрешение нет смысла, так как подобные рекламные щиты рассматриваются с большого расстояния. При таких условиях увидеть разницу между 12 и 120 Мп просто невозможно. Да и сами принтеры печатают на билборды с очень маленьким количеством капель на дюйм (dpi).

Поэтому, конечно же, реклама Samsung выглядит просто несерьезной, как и сама идея использовать смартфон с 200-Мп камерой для подобных задач.

Но мы понимаем, что мегапиксели в теории очень важны. Как минимум, такое высочайшее разрешение позволит нам иметь аналог оптического приближения без потерь качества. То есть, одна камера может сразу выполнять роль как основной, так и 5-кратного телеобъектива.

Более того, мы можем делать кадрирование уже после съемки, обрезая ненужные части кадра без ущерба качеству. Или же можно печатать снимки больших размеров, которые будут рассматриваться с очень близкого расстояния и т.д.

Вопрос лишь в том, способен ли смартфон выдать такое разрешение.

Мобильный объектив, дифракция и нано-пиксели

Сразу же хочу сказать то, что шокирует многих противников мобильной фотографии. Точнее, приведу дословную цитату из документа, подготовленного уважаемой компанией Carl Zeiss¹:

Разрешающая способность небольшой мобильной оптики значительно превосходит лучшие 35-мм объективы

Другими словами, мобильный объектив Carl Zeiss, установленный в «древней» Nokia N8 2011 года выпуска, до сих пор превосходит по резкости дорогие профессиональные объективы.

Если вы умеете читать графики частотно-контрастной характеристики (MTF) объективов, то знаете, что тесты современной профессиональной оптики делаются на разрешении до 30 lp/mm (30 пар линий на миллиметр).

То есть, мы проверяем, насколько хорошо объектив способен передать контраст очень тонких линий (30 черных и 30 белых линий, помещающихся в одном миллиметре) или насколько хорошо разделяются эти линии:

Так вот, для мобильного объектива разрешить 30-40 пар линий на миллиметр — это вообще «ни о чем». Такие крохотные объективы превосходно справляются с 80 lp/mm и выше.

Для тех, кто понимает MTF-графики, просто приведу пример теста старенькой (11-летней давности) мобильной линзы от компании Carl Zeiss:

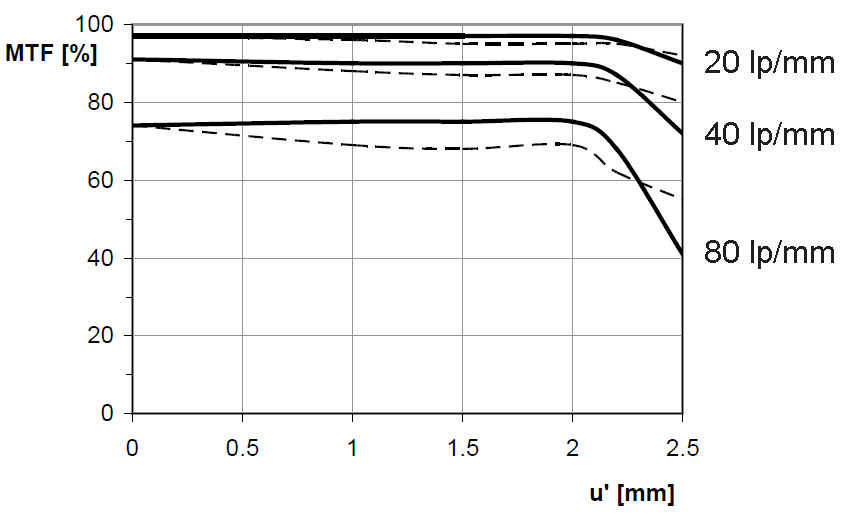
Если же вам этот график ни о чем не говорит, то просто знайте, что популярное мнение касательно превосходства в плане резкости профессиональных объективов — это миф.

Верно обратное — мобильные дешевые объективы дают картину в разы более резкую и детализированную, чем профессиональные объективы больших камер.

Почему так происходит?

Прежде всего, это связано с тем, что объектив находится очень близко к матрице (буквально в 5-7 миллиметрах) и проецирует очень маленькое, но при этом очень детальное изображение.

Чтобы осознать это интуитивно, представьте проектор. Чем сильнее мы отдаляем его от стены, тем крупнее и размытее становится изображение. И наоборот, чем ближе проектор к стене, тем меньше и чётче становится вся картинка. Так и с объективами.

Дифракция света и нано-пиксели

Как вы думаете, существует ли абсолютный предел четкости, за который никогда не выйдет ни один объектив? Да. И называется он дифракционным пределом.

Если вы забыли данный термин, то напомню, что дифракция — это свойство света огибать препятствия на своем пути.

Свет можно представить как жидкость. К примеру, если на пути световой волны будет стоять маленькое препятствие, то волна его просто обойдет. А если волна столкнется со стеной, в которой есть маленькое отверстие, то она пройдет через отверстие и начнет расходиться в стороны:

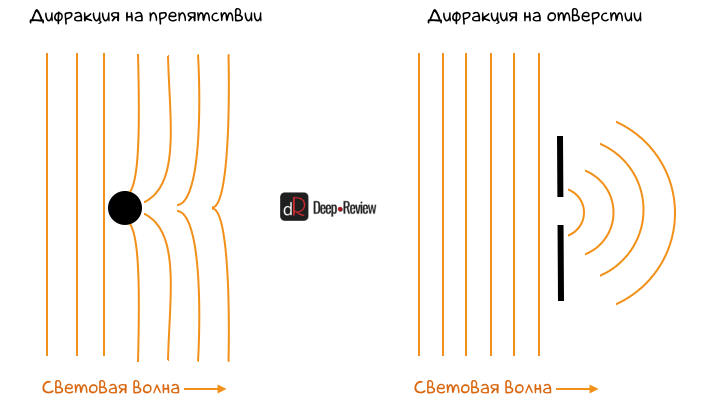
Когда мы говорим о фотографии и объективах, нас волнует именно второй случай — прохождение света через небольшое отверстие (объектив).

Чем меньше это отверстие, тем сильнее будет выражена дифракция, то есть, тем сильнее свет будет расходиться в стороны и оставлять более размытые пятна на матрице.

Соответственно, у нас не получается сфокусировать очень крохотную точку на мобильном сенсоре, так как свет от точки, пройдя через отверстие камеры, начнет «расплываться» в стороны и вместо этого мы получим размытый след.

Более того, световые волны начнут накладываться друг на друга и мы получим не просто размытую точку на матрице, а так называемый узор Эйри — это яркое большое пятно (диск Эйри) с концентрическими кольцами вокруг:

Какой бы маленькой ни была точка в реальном мире и каким бы качественным/дорогим ни был объектив, существует минимальный размер диска Эйри — минимальный диаметр центрального пятна узора Эйри, меньше которого сфокусировать свет не получится.

Отчего же зависит этот теоретический предел? Исключительно от трех вещей:

• Длины волны света
• Размера отверстия в объективе, через который проходит свет
• Расстояния от объектива до матрицы

Длина волны зависит от цвета (точнее, цвет зависит от длины волны) и может варьироваться примерно от 0.4 до 0.7 мкм. Синий цвет — это короткие волны (до 0.48 мкм), зеленый — это волны до 0.55 мкм, красные цвета самые «длинные» и могут достигать размера 0.7 мкм.

Чем короче волна, тем меньшее пятно света можно сфокусировать. Соответственно, если мы будем работать только с красным светом, то минимальное пятно (диск Эйри) будет большего размера, чем если бы мы работали с синим цветом.

В этой связи можно вспомнить компакт-диски. Первые CD использовали лазер красного цвета для чтения и записи информации. Поэтому существовал определенный минимальный размер дорожки, которую этот лазер мог выжигать.

Затем производители заменили красный лазер на синий, что позволило значительно сократить диаметр диска Эйри и размер дорожки, тем самым в разы увеличив объем памяти. Ведь дифракция позволяла сфокусировать пятно меньшей площади благодаря свету с более короткой длиной волны. Новую технологию так и назвали Blu-Ray (от англ. синий луч).

Но вернемся к объективам.

Как же нам посчитать минимальный размер пятна, которое конкретный объектив способен сфокусировать на матрице?

Рассчитываем дифракционный предел

Диск Эйри (напомню, это размытое пятно, в которое превращается чёткая точка, когда свет проходит через отверстие объектива) измеряется в угловых размерах.

Почему в угловых? Да потому, что расходящийся в стороны пучок света оставит разные по размеру следы на матрице в зависимости от того, как далеко эта матрица будет находиться от объектива:

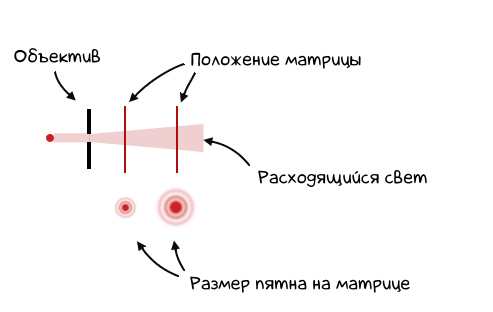
Если матрица будет находиться очень близко, свет просто не успеет достаточно «расплыться» в стороны, чтобы оставить широкие пятна. В результате мы будем видеть очень маленькие «пятнышки».

Именно поэтому удобно использовать угловой размер пятна света, который рассчитывается по формуле:

θ = 2.44 * λ / D

Здесь: θ — это угловой размер (в радианах), λ — длина волны, а D — диаметр отверстия объектива.

Но, согласитесь, использовать эту формулу не очень удобно. Многие люди попросту не понимают, что такое угловой размер и как его перевести в привычные нам миллиметры или микрометры. Кроме того, нужно знать диаметр мобильного объектива.

Поэтому на основе простых геометрических соотношений можно изменить эту формулу, сделав её более понятной каждому человеку:

d = 2.44 * λ * N

Здесь: d — это диаметр пятна света (диска Эйри) в привычных миллиметрах/микрометрах, λ — длина волны (можно брать зеленый цвет как среднее значение — 0.55 микрометров), а N — это относительное отверстие объектива — те самые f/1.8 или f/2.4, которые указаны в характеристиках камеры любого смартфона.

Теперь посчитать нужное нам значение не представляет никакой сложности.

Для примера возьмем объектив Samsung Galaxy S22 Ultra. В технических характеристиках видим относительное отверстие его основной камеры — f/1.8. Подставляем эти значения в формулу:

d = 2.44 * 0.55 * 1.8

Получаем результат 2.4 мкм. Это и будет минимальный диаметр пятна света, которое мобильный объектив способен спроецировать на матрицу Galaxy S22 Ultra.

Но ведь мы знаем, что размер пикселя 108-Мп камеры Galaxy S22 Ultra составляет 0.8 мкм, что в 3 раза меньше! Получается, никакого смысла в таких маленьких пикселях нет? Ведь минимальная деталь на фото (минимальный размер пятна света) будет всегда в 3 раза крупнее пикселя:

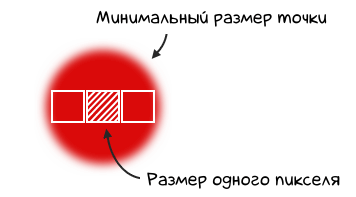
На самом деле, всё не так просто и об этом знали еще бароны в 1879 году.

Критерий третьего барона Рэлея

Когда два пятна света начинают сближаться друг с другом, до какого-то момента мы еще можем их различить. И Джон Стретт, более известный по своему титулу (третий барон Рэлей), определил момент, когда сделать это становится почти невозможной задачей.

Согласно так называемому критерию Рэлея две точки еще можно различить, если центры их дисков Эйри (размытых пятен) разделены радиусом диска Эйри. Когда же расстояние между двумя пятнами становится меньше их радиуса, изображение двух точек сливаются в одно пятно:

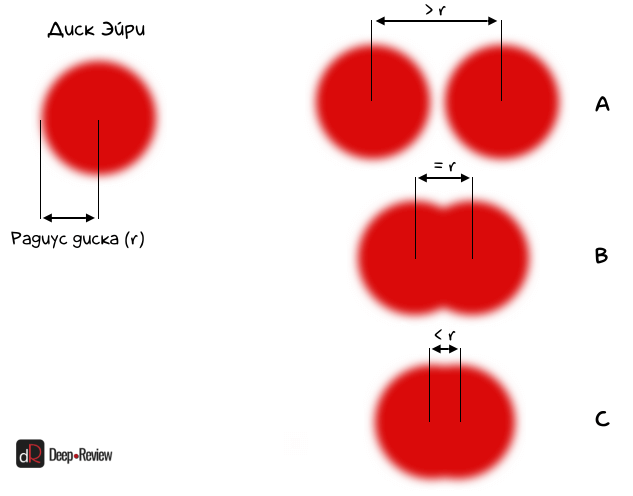
На этой иллюстрации мы видим, что в первом случае (A) две точки различаются превосходно, так как находятся далеко друг от друга.

Во втором случае (B) расстояние между пятнами равняется их радиусу и это критический момент, когда отдельные пятна еще различимы. Третий вариант (C) — две точки слились в одно пятно, так как расстояние между ними меньше их радиуса.

Из этого мы можем сделать вывод, что минимальный размер объекта, который можно различить на матрице, равен радиусу диска Эйри. То есть, объекты различимы, пока между ними есть расстояние, равное радиусу диска Эйри.

К слову, выше в статье я упоминал о разрешении объективов, измеряемом в парах линий на миллиметр или lp/mm. Так вот, радиус диска Эйри — это и есть та самая одна пара линий (lp).

Теперь нам нужно вместо рассмотренной выше формулы диаметра диска Эйри, использовать радиус, то есть, разделить выражение (2.44 * λ * N) на два, так как радиус — это половина диаметра. Получаем:

r = 1.22 * λ * N

По этой финальной формуле и вычисляется так называемый оптический предел разрешения объектива. Забегая наперед, скажу, что речь идет исключительно об «идеальном объективе», то есть, это теоретический предел, связанный с дифракцией.

Соответственно, в теории объектив Galaxy S22 Ultra способен различить две отдельные точки, если расстояние между ними не будет превышать 1.2 мкм для зеленого цвета с длиной волны 0.55 мкм (r = 1.22 * 0.55 * 1.8).

Что ж, получается, нет смысла в случае с Galaxy S22 Ultra делать пиксели размером менее 1.2 мкм, ведь это оптический предел разрешения? Не совсем так.

Теория цифровой обработки сигналов

На самом деле есть еще одна очень важная деталь, которую следует знать, прежде, чем говорить о размере пикселя.

Когда мы записываем звук или делаем снимок на смартфон, мы фактически пытаемся записать непрерывный сигнал в виде отдельных и независимых друг от друга (дискретных) значений.

В результате мы сталкиваемся с довольно серьезной проблемой. Ведь мы не можем выделять для одной картинки бесконечное количество информации, чтобы записать положение, условно говоря, каждого атома.

Представьте, что объектив проецирует на матрицу изображение красного сердечка и мы хотим оцифровать его:

Как нам это сделать?

Можно разбить всю матрицу, скажем, на 9 одинаковых клеточек — так называемых «пикселей». Теперь нужно смотреть в центр каждой клетки (показано на рис. черной точкой) и проверять, какой здесь цвет.

Если красный — окрашиваем всю клеточку/пиксель в красный цвет (мы не можем окрасить только часть пикселя — либо всё, либо ничего). Если же цвета нет — оставляем пиксель неокрашенным. В итоге получим такой результат:

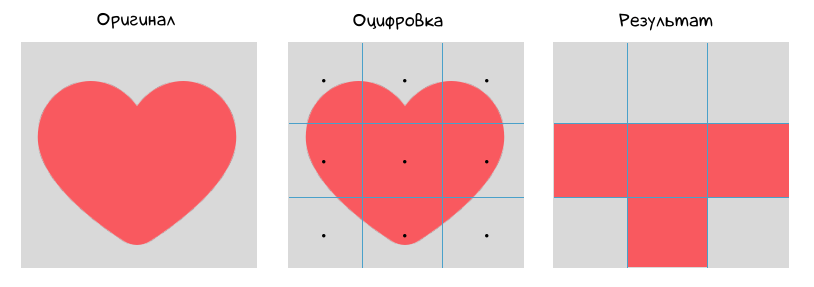
Согласитесь, оцифрованный результат имеет мало общего с первоначальным сердечком. Это и понятно, ведь 9 пикселей явно недостаточно для точной передачи изображения. А сколько же пикселей нужно брать?

Другими словами, с каким шагом нужно сканировать изображение, чтобы оцифровывать его? Будем анализировать цвет каждый миллиметр или каждый микрометр? А может лучше вообще взять нанометр?

На самом деле, ответ на этот вопрос уже давно существует и сформулирован он в теореме Котельникова (или Найквиста-Шеннона).

Если говорить об оцифровке изображения, тогда минимальный шаг должен равняться половине размера самой мелкой детали оригинала.

Как мы уже определили, самая мелкая деталь изображения на матрице равняется радиусу диска Эйри. Соответственно, чтобы передать эту деталь без искажения, нужно иметь минимум 2 пикселя на радиус. Но это самый необходимый минимум, а лучше и вовсе иметь 3 пикселя на радиус.

Только в этом случае матрица не станет ограничивающим фактором.

Мы уже посчитали, что в теории из-за дифракции объектив Galaxy S22 Ultra способен сфокусировать диск Эйри с минимальным радиусом в 1.2 мкм. Согласно теореме Котельникова, нам нужно иметь минимум 2 пикселя на этот радиус, а значит, нужны пиксели размером 0.6 мкм!

А если говорить об идеальном варианте, то размер пикселя и вовсе должен составлять 0.4 мкм (3 пикселя на радиус диска Эйри, в нашем случае радиус = 1.22 мкм)!

Но всё это только в теории. То есть, если исключить массу других факторов, то в новом 200-Мп сенсоре ISOCELL HP3 размер пикселя идеален с точки зрения цифровой обработки сигнала. Он составляет всего 0.56 мкм при необходимом минимуме в 0.6 мкм.

А красный свет «влезет» в такой пиксель?

Прежде, чем мы перейдем к печальным выводам, хочу еще буквально два слова сказать о том, сможет ли красный цвет с длиной волны 0.6 мкм поместиться в пиксель размером 0.4 или 0.1 мкм.

Если мы схематически нарисуем световую волну большой длины и крохотный пиксель, то поставленный выше вопрос должен сразу отпасть:

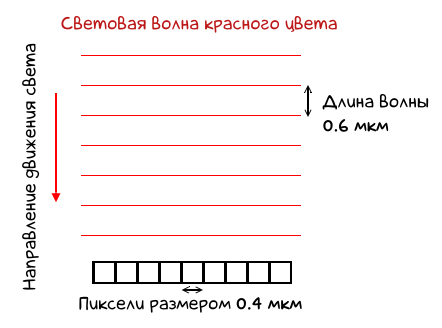
То есть, мы видим, что по всей ширине волна непрерывна и накрывает пиксели, какими бы маленькими они ни были. Длина волны — это, скорее, частота, с которой отдельные волны «ударяются» в пиксель. Чем длиннее волна, тем больше времени проходит между тем, как очередной «гребень» столкнется с пикселем. Вот и всё!

В конце концов пиксель «ловит» отдельные фотоны света. А у фотона-то и размера как такового нет. Это безмассовая фундаментальная частица, которая точно меньше любого физического объекта во вселенной, чем является кусочек кремния под названием пиксель.

Так что переживать о том, что крупный красный фотон не «влезет» в крохотный пиксель, явно не стоит. Не стоит думать о длине волны света как о размере фотона.

Достигла ли новая 200-Мп матрица Samsung лимита разрешения?

Всё это время мы рассматривали идеальный сценарий, игнорируя массу проблем и особенностей реальных сенсора и объектива.

Размер статьи не позволяет нам глубоко окунуться в эти проблемы, поэтому я постараюсь лишь тезисно их очертить:

Неидеальные линзы. На самом деле диск Эйри не всегда выглядит так красиво, а его диаметр не всегда равняется расчетным значениям. Дело в том, что помимо дифракции все объективы в той или иной степени дают такие искажения, как:

• Сферические аберрации
• Хроматические аберрации
• Кома
• Астигматизм
• Кривизна поля изображения
• Дисторсия

Добавьте к этому проблемы со стабилизацией или автофокусом на микро-уровне, что приводит к размытию изображения в масштабах микрометров.

Всё это может значительно увеличивать минимально различимый объект на матрице, а потому добиваться минимального размера пикселя зачастую бессмысленно. Особенно, когда речь идет о смартфонах, а не медицинских микроскопах.

Особенности современных матриц. Мы говорили о том, что в идеале размер одного пикселя должен составлять половину радиуса диска Эйри.

Но когда мы говорим о той же матрице ISOCELL HP3, то нужно понимать, что здесь пиксели собраны по 16 штук под одним цветным фильтром.

То есть, ширина цветного фильтра составляет 2.24 мкм (4 пикселя * 0.56 мкм). Соответственно, такой цветной пиксель превышает в 2 раза радиус диска Эйри.

Другими словами, даже с учетом 200 мегапикселей, «цветного разрешения» такой матрицы не достаточно для данного объектива. В цвете такая матрица может оцифровать минимальное пятно света радиусом в 5 мкм. А значит, что ни о каких 200-Мп даже речь не идет.

Более того, мы не можем просто сокращать размер пикселя в погоне за разрешением. Ведь с уменьшением пикселя мы уменьшаем динамический диапазон и увеличиваем уровень шума.

Первая проблема решается за счет различных ухищрений, вроде съемки с разной выдержкой каждого пикселя в группе или съемки с несколькими последовательными затворами. А проблему шума частично решают биннингом пикселей. Но при этом значительно падает разрешение.

Более того, сколько бы ни было мегапикселей на матрице, каждый пиксель считывается отдельно. В случае с 200-Мп матрицей ISOCELL HP3 при каждом снимке считываются все 200 млн фотодиодов по отдельности, даже если вы снимаете в режиме биннинга 16-в-1 с разрешением в 12 Мп. Это просто особенности технологии CMOS.

Из-за этого в разы возрастает требования к вычислительной мощности смартфона. Нужно не только считывать несколько сотен миллионов пикселей, но и обрабатывать их.

Кроме того, если снимать в режиме 200-Мп, тогда возрастает и размер одного файла. Он легко может достигать 60 Мб и выше. Соответственно, растет требование к памяти. И ради чего всё это?

Одним словом, бесконечно уменьшать пиксель в погоне за разрешением — довольно глупая затея. Хотя в теории это можно делать вплоть до 0.3 мкм, если работать над уменьшением диска Эйри (например, разработать объектив с f/1.2).

Так почему же производители это делают?

Как минимум на это есть три причины:

• Экономия. Делать маленькие пиксели очень удобно, если из этих пикселей складывать небольшие по размеру сенсоры. Samsung может опробовать 0.56-мкм пиксели на 200-Мп матрице, а затем выпустить на базе этих же пикселей 48-Мп матрицу крошечного размера. А чем меньше матрица, тем больше их можно нарезать из одной пластины, что значительно сокращает себестоимость сенсора.
• Удобство для производителей. Производители смартфонов не хотят делать толстые устройства, а именно модуль камеры является одним из самых толстых элементов смартфона. Маленькие пиксели позволяют сократить размер матрицы и, соответственно, фокусное расстояние объектива, чтобы он не выступал за пределы корпуса.
• Маркетинг. По большому счету, нет никакой разницы, будете ли вы просматривать на маленьком экране смартфона 12-Мп снимок или 200-мегапиксельный. Но для обывателя камера на 200-Мп звучит на порядок внушительней. Покупатели в подавляющем большинстве ничего не понимают в физике камер, они обращают внимание только на цифры.

В общем, если делать выводы из статьи, то я бы сказал следующее. В крохотных 0.56-мкм пикселях теоретически есть смысл. В паре с идеальным объективом f/1.8 они способны значительно увеличить детализацию изображения.

Но практического смысла в этом нет. Даже с учетом вычислительной фотографии.

Было бы куда лучше остановиться на 48 мегапикселях (в отличие от полнокадровых зеркалок для мобильного объектива 12 мегапикселей всё же слишком мало) и доводить их до ума: увеличивать размер и ёмкость (динамический диапазон), повышать «светочувствительность» (квантовую эффективность), экспериментировать с цветными фильтрами и работать над качеством оптики.

Однако в реальности мы будем наблюдать другое — всё более агрессивную обработку нейросетями и дальнейшее уменьшение пикселей. Как минимум, 0.4-мкм — вполне ожидаемый размер в ближайшие год-два.

Эта тема слишком обширна и сложна, чтобы раскрыть её в одной статье, но, надеюсь, после прочтения данного материала вы узнали что-то новое о мегапикселях и объективах.

Алексей Сало, главред Deep-Review