Работая над обзором новых TWS-наушников Sony WF-1000XM3, я столкнулся с одним интересным явлением. Эти наушники, как и многие другие устройства от Sony, поддерживают фирменную технологию DSEE HX, которая, согласно заявлениям самой компании, «творит чудеса» со звуком.
Но мой интерес вызвала не столько технология, сколько отношение к ней популярных ресурсов с обзорами техники.
Если какой-то автор не забывал упомянуть о DSEE HX, то это обязательно был хвалебный отзыв, повторяющий описание, прочитанное на официальном сайте Sony, которое гласит:
DSEE HX улучшает качество сжатого с потерями MP3-файла до уровня Hi-Res Audio, восстанавливая утерянные параметры оригинальной записи.
Официальное «объяснение» технологии DSEE HX
Другими словами, больше не нужны lossless-файлы в формате 24 бит/96 кГц (или 24/192), достаточно взять обычный сжатый mp3-файл в формате 16 бит/44.1 кГц, включить функцию DSEE HX и на выходе получаем тот же Hi-Res-аудио формат!
Сразу сделаю небольшую оговорку. Если вы не понимаете, о чем я только что написал и все эти «биты» и «килогерцы» ни о чем вам не говорят — прекрасно! К концу статьи вы будете очень хорошо во всем этом разбираться.
Но прежде, чем говорить о технологии Sony DSEE HX, нужно кое-что прояснить.
Как выглядит цифровой звук
Обычный (не цифровой) звук — это не более, чем столкновение молекул воздуха друг с другом. Когда, к примеру, мы хлопаем в ладоши, молекулы воздуха разделаются в разные стороны и ударяют по соседним молекулам:
Те, получив импульс, толкают следующие молекулы и так до тех пор, пока эти столкновения не попадут к нам в ухо и не ударят по барабанной перепонке. Если вы об этом не знали, тогда можете почитать вот эту нашу статью.
В результате таких столкновений в пространстве создаются области сжатого и разреженного воздуха (где молекулы сбились в кучу — это сжатый воздух, а где между ними образовалось много свободного пространства — разреженный).
Такие участки сжатия и разряжения мы обозначаем в виде волны — чем выше волна, тем сильнее в этом участке сжатие воздуха и наоборот, чем ниже опускается волна, тем более разрежен воздух:
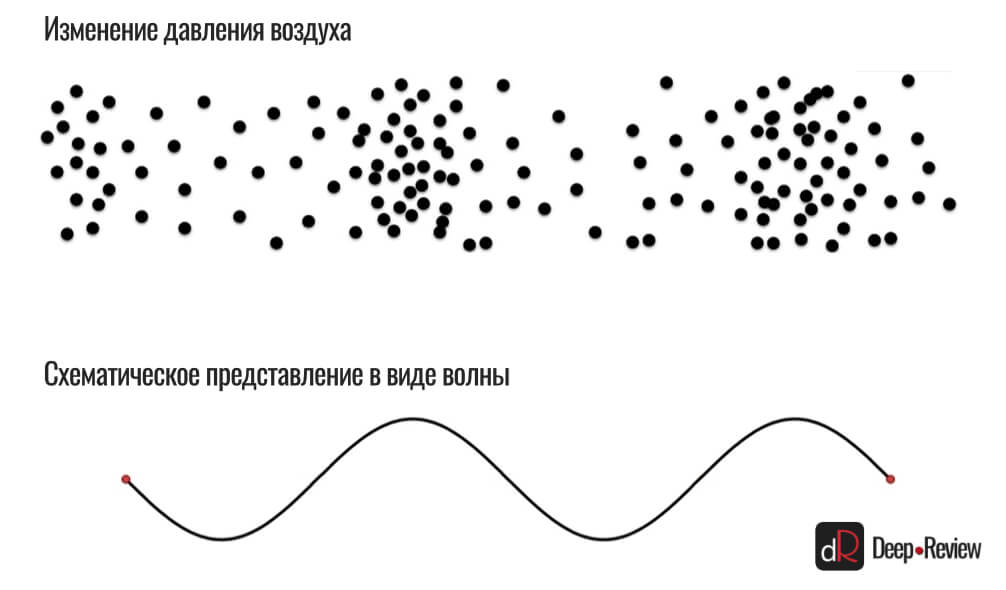
Теперь представьте следующую звуковую волну, которую нам необходимо оцифровать (записать в виде нулей и единичек), чтобы сохранить на смартфоне и в дальнейшем воспроизводить:
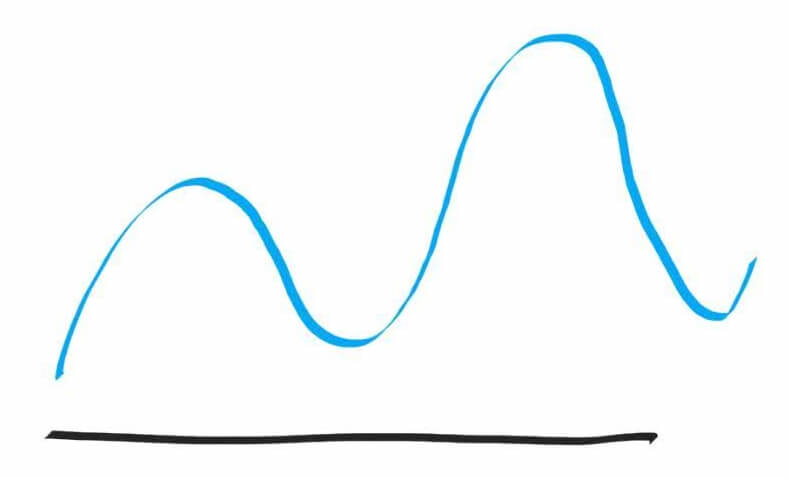
Черная линия на картинке — это промежуток времени, равный 1 секунде. Когда микрофон записывает звук, в его мембрану ударяются те самые молекулы, что бьют и по нашей барабанной перепонке. И это движение мембраны преобразовывается в электрическое напряжение.
Всё, что нам нужно сделать — это записать значение напряжения в каждый конкретный отрезок времени и сохранить в бинарном виде (нули и единицы). Но как часто это делать?
Для простоты решим, что мы будем делать 5 замеров или «снимков» (сэмплов) и сохранять их в файл. В течение одной секунды мы 5 раз измерим напряжение через ровные промежутки времени, т.е. каждые 200 миллисекунд будем проверять напряжение и сохранять его значение:
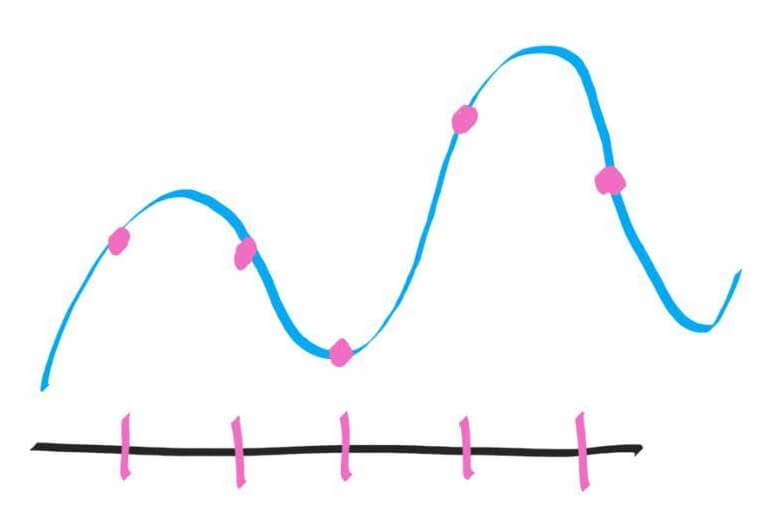
Розовым цветом показаны те значения амплитуды (силы удара молекул о мембрану или, по-простому, громкости звука), которые мы запишем. В результате, если в течение секунды сделать всего 5 замеров, тогда в цифровой записи от красивой плавной звуковой волны у нас останется лишь это недоразумение (мы просто соединили розовые точки):
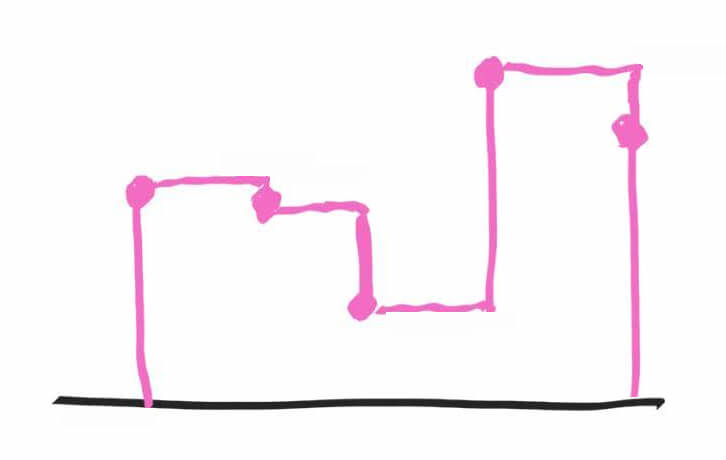
Согласитесь, это не совсем то, что было в оригинале. И если теперь такую запись попытаться снова преобразовать в аналоговый сигнал, качество звука будет совершенно неприемлимым.
Что же делать? Естественно, нужно чаще делать «снимки» (сэмплы) звуковой волы, то есть, за одну секунду записывать значение напряжения в 2 раза чаще:
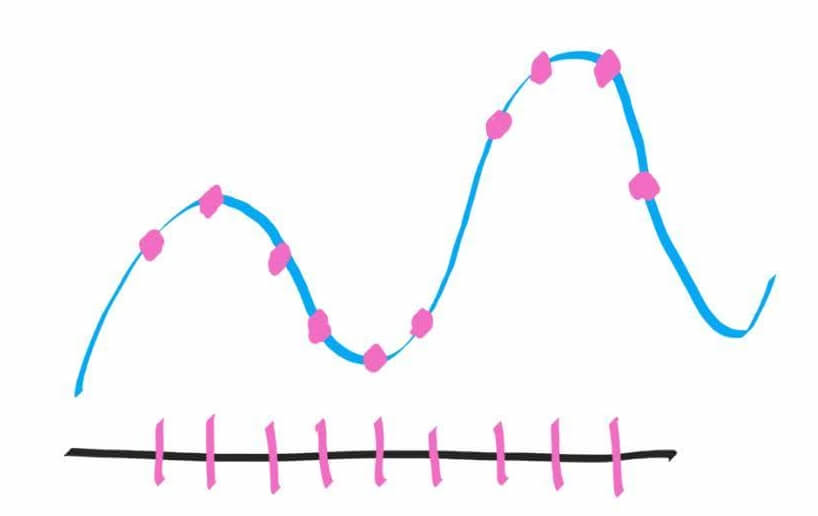
Теперь на записи мы получим немножко более детализированную картинку, которая будет больше похожа на оригинал, но все еще далека от него:
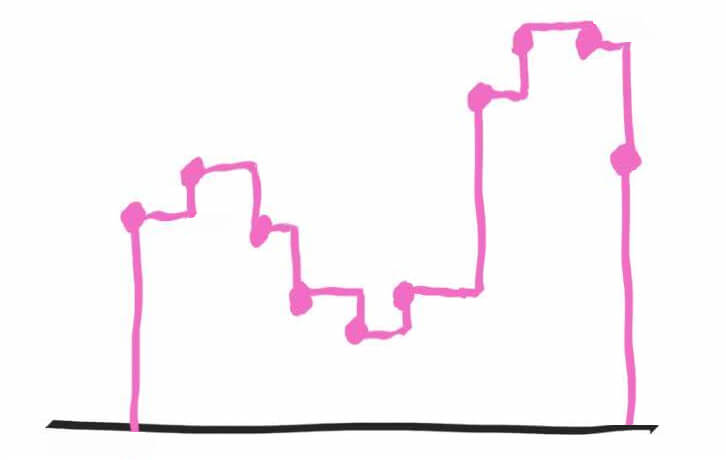
Чтобы максимально приблизиться к оригиналу и записать все звуки в точности, как они звучали в реальной жизни, нам нужно гораздо чаще делать сэмплы (снимки) аналогового сигнала.
Так вот, частота, с которой мы записываем напряжение сигнала, называется частотой дискретизации. Если мы говорим, что частота дискретизации равняется 100 Гц (1 Гц = 1 раз в секунду), это означает, что за секунду мы делаем 100 замеров (сэмплов) звуковой волны. Если будем записывать значение напряжения 1000 раз в секунду, получим частоту дискретизации 1 кГц и т.д.
Если частота дискретизации будет не достаточно высокой, мы можем часто пропускать пики и впадины звуковой волны, что в итоге отразится на качестве звука. То есть, низкая частота дискретизации главным образом разрушает информацию и детализацию верхнего частотного диапазона, где длина волны очень короткая и между двумя замерами может запросто вместится несколько волн.
Так какая же частота дискретизации у обычного MP3-файла? Сколько «снимков» в секунду хранится в таком формате? Для начала нужно понимать, что MP3-файл — это уже сжатый с потерями Audio CD. Стандартом для CD-качества является частота дискретизации 44.1 кГц (44 100 сэмплов в секунду). Соответственно, MP3-файл имеет такую же частоту дискретизации, то есть, 44 100 Гц.
Разрядность или глубина кодирования звука
Но есть еще один важный параметр, влияющий на качество записи звука, под названием разрядность. Чтобы понять, что это такое, давайте еще раз вернемся к примеру нашей звуковой волны:

Здесь мы устанавливали розовые точки прямо по линии звуковой волны через определенные промежутки времени. Образно говоря, мы смогли поставить розовую точку на любой высоте, то есть, каждую пятую часть секунды мы считывали сигнал очень точно.
Но теперь представьте, что вы не можете поставить точку по высоте в любом месте, не можете считать сигнал с идеальной точностью. Вместо этого у вас есть всего 3 возможных варианта (зеленые отметки по оси Y):
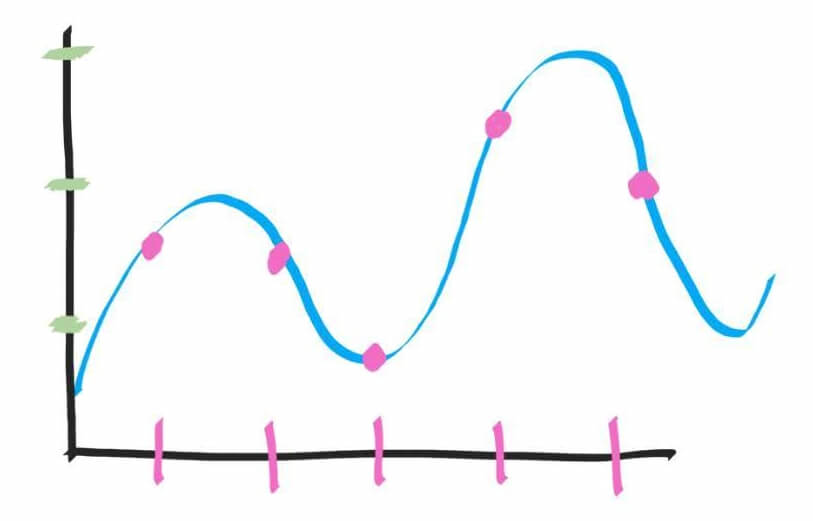
И теперь нужно ставить точку не прямо на волне, то есть, считывать не идеально точно, а приблизительно, по вертикальным зеленым отметкам. В итоге у нас получится оцифровать аналоговый сигнал следующим образом:
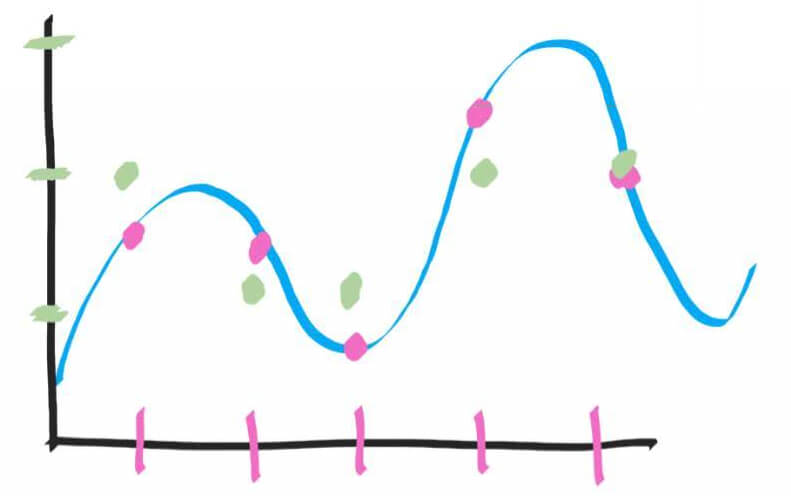
Теперь удалим все лишнее и полюбуемся цифровой записью (слева — аналоговый оригинал, а справа — то, что получилось в итоге):

Не нужно быть специалистом, чтобы понять, что цифровая копия не очень соответствует оригиналу.
И здесь мы подходим к понятию разрядности или глубины звука, которая выражается в битах. Разрядность и показывает, с какой детализацией мы можем записать значение напряжения (или амплитуды) в каждый конкретный момент. Недостаточно лишь увеличивать частоту считывания аналогового сигнала, нужно делать это с высокой детализацией.
Представьте, что теперь у нас на оси ординат не 3 отметки, а 300 или 3000 отметок. Это позволит нам с высочайшей точностью записать значение сигнала и параллельно увеличит динамический диапазон записи.
Именно поэтому разрядность (битность) еще называют динамическим диапазоном звука, так как чем выше эта разрядность, тем сильнее будет разница между самым громким и самым тихим звуком на записи.
Небольшой итог
К этому моменту вы уже должны хорошо представлять себе разницу между файлом, записанным в формате 16 бит/44.1 кГц и 24 бита/96 кГц.
В первом случае при записи использовалась разрядность 16 бит. То есть, при записи амплитуды (напряжения) было доступно ~65 тыс. возможных значений (это и есть 16 бит или 2 в 16 степени). А частота дискретизации равнялась 44.1 кГц, то есть, оборудование записывало значение напряжения 44 100 раз в секунду.
Во втором случае при записи использовалась разрядность 24 бита (всего ~16 млн возможных значений для каждого сэмпла) и частота сэмплирования составляла 96 тысяч раз в секунду.
Другими словами, запись в формате 24 бита/96 кГц содержит гораздо больше реальной информации о звуке, чем та, что записывалась в формате 16 бит/44.1 кГц. При использовании 24 бит нам доступно 16 млн значений для записи громкости. Это и есть динамический диапазон или разница в 16 млн раз между самым тихим значением громкости (условно единица) и самым высоким (условно 16 777 216 единиц). Вопрос лишь в том, нужна ли вся эта дополнительная информация. Но об этом чуть позже.
Что же такое Sony DSEE HX на самом деле?
Теперь, когда мы разобрались со всеми этими терминами, пришло время ответить на главный вопрос — что же такое в действительности технология DSEE HX?
DSEE HX — это алгоритм повышения частоты дискретизации сжатого mp3-файла с 44.1 до 96 кГц и разрядности с 16 до 24 бит
Другими словами, после обработки самого простого mp3 файла алгоритмом DSEE HX, аудиозапись будет содержать в 2 раза больше информации (только не в самом файле, а в оперативной памяти)!
Представьте, что у вас появилась возможность каким-то чудом вернуться в момент записи оригинальной песни и перезаписать ее с гораздо более высокой детализацией, чтобы она содержала всю ту информацию, что была потеряна при записи с более низкой частотой дискретизации и разрядностью, а также сжатием файла.
Думаю, каждый понимает, что сделать это невозможно. Если какой-то информации в файле нет (скажем, после сжатия с потерями), она там и не появится. По крайней мере, при современном развитии технологий. Возможно, в будущем искусственный интеллект и нейросети смогут это делать, анализируя композицию и добавляя реальную информацию, которая была потеряна. Но, не сегодня и не «на лету», как это делает DSEE HX.
Откуда же DSEE HX берет информацию?
Примерно оттуда же, откуда и все другие апскейлеры — математика. То есть, для вычисления промежуточных значений используется интерполяция. Мы также умеем интерполировать — если мы видим 2 высокие ступеньки, поднимающиеся вверх, нам ничего не мешает добавить между ними еще 2 ступеньки размером поменьше:
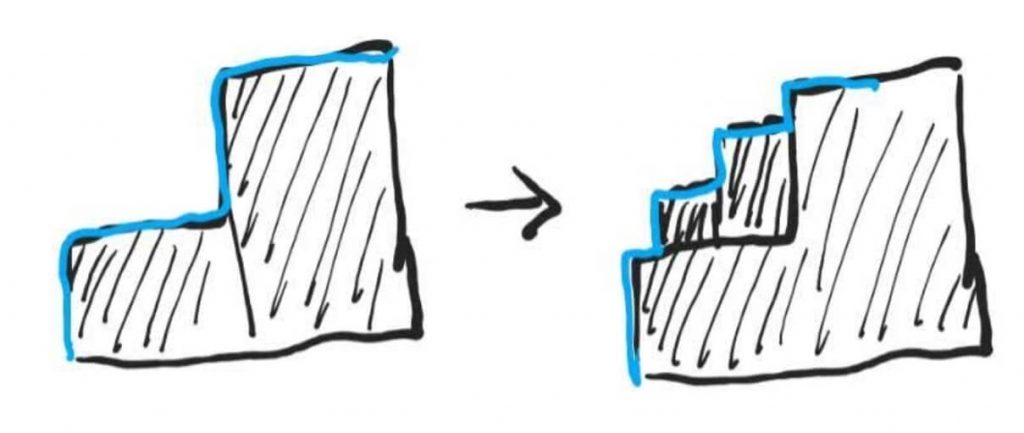
Что изменилось? Общая высота подъема или угол подъема? Ничего! Только ступенек стало в два раза больше. Примерно то же делает и DSEE HX, увеличивая частоту дискретизации и разрядность, но не добавляя никакой полезной информации в звук, тем более той, что была утрачена при сжатии.
Проблема в том, что делать простое сглаживание не означает оцифровывать звук с более высокой частотой. В реальности между двумя ступеньками мы могли пропустить целую волну очень высокой частоты. А алгоритм просто сгладил эти ступеньки, даже не догадываясь о ее существовании.
Так что же это получается, все дело в маркетинге? Давайте перед ответом на этот вопрос обсудим кое-что еще.
Какой может быть максимальная частота дискретизации и разрядности?
Можно ли увеличивать частоту дискретизации до бесконечности, улучшая тем самым качество звука? Вот мы считываем аналоговый сигнал 44 тысячи раз в секунду и оцифровываем звук. А если сэмплировать сигнал 1 миллион раз в секунду, будет ли от этого качество звука выше в 20 раз? Ведь, по идее, даже разница в 2 раза будет слышна каждому, а в 20 и подавно!
К сожалению, так это не работает. Вернее, работает, только толку нам, как слушателям, от этого никакого нет. Дело в том, что человек теоретически способен слышать звуки в диапазоне от 20 Гц до 20 кГц (20 000 Гц), причем с возрастом верхняя граница постоянно снижается.
Подавляющее большинство авторов, которые успели «насладиться» работой DSEE HX, к сожалению, физически не способны были услышать никаких звуков с частотой свыше 16 кГц. Да и вы с вероятностью в 99% не услышите ничего на частоте 17 кГц и выше. Если, конечно, вам не 6 лет.
Тут еще очень важно отметить тот факт, что DSEE HX, как и высокая частота дискретизации в целом, имеет дело именно с верхней границей частотного диапазона. То есть, увеличивая частоту дискретизации, мы добавляем детализацию исключительно в верхних частотах. Но как бы мы не детализировали ультразвук, приятнее от этого композиция звучать не будет, а вот размер файла увеличится заметно.
Какие частоты звукового диапазона сохраняются в mp3-файле?
А теперь самое интересное. Как вы считаете, какую максимальную частоту звука возможно оцифровать и записать в файл (сэмплировать), используя стандартную для многих mp3-файлов частоту дискретизации 44.1 кГц?
К счастью, нам не нужно ничего высчитывать и доказывать, с этим успешно справились Гарри Найквист в 1928 году и Владимир Котельников в 1933 году. Так вот, согласно теореме Котельникова, при оцифровке аналогового сигнала (при дискретизации), частота дискретизации должна быть в два раза выше частоты звука, которую мы хотим записать.
Перефразирую еще по-другому. Для того, чтобы без единой потери записать звуки определенной частоты в цифровом виде, нужно считывать значение напряжения в 2 раза выше этой частоты.
Если предположить, что существуют взрослые люди со сверхспособностью слышать звук на частоте 20 000 Гц, тогда частота дискретизации при сэмплировании должна равняться минимум 40 000 Гц (40 кГц). А теперь еще раз вспомним, что частота дискретизации у mp3 — 44 100 Гц (44.1 кГц), что заметно превышает необходимую частоту для подавляющего большинства слушателей. То есть, используя частоту дискретизации 44.1 кГц мы можем записать весь слышимый частотный диапазон, вплоть до ультразвука на частоте 22 000 Гц.
Другими словами, записав аналоговый звук в цифровом виде с частотой дискретизации 44.1 кГц, мы можем заново воспроизвести оригинал без малейших искажений. И пусть в цифровом виде будет «лесенка», а не плавная звуковая волна. После прохождения реконструкционного фильтра любого ЦАПа (цифро-аналогового преобразователя), мы получим идеально гладкий аналоговый сигнал, который будет в точности соответствовать оригиналу.
Но, повторюсь, весь смысл mp3-формата в том, чтобы сжать аудиоданные, внося определенные потери. И если мы говорим про mp3-файлы с битрейтом 320 кбит/с, тогда услышать разницу между mp3 и оригиналом (16 бит/44.1 кГц) очень тяжело. Даже если использовать дорогое оборудование, люди, занимающиеся звуком профессионально, при очень внимательном прослушивании, далеко не всегда смогут определить на слух хоть какую-то разницу.
Ну всё, теперь Sony нас точно обманула!
Не только люди неидеальны, но и аппаратура. Если бы мы записывали звук с частотой дискретизации 44.1 кГц и разрядностью 16 бит, его качество оставляло бы желать лучшего.
Каждый человек мог бы слышать разницу в звучании композиции, записанной в формате 44.1 кГц/16 бит и 96 кГц/24 бита. И суть не в том, что одна запись содержала бы больше полезной (слышимой) информации. Все дело в искажениях и ошибках, которые вносит аппаратура (фильтры) и программное обеспечение при работе со звуком.
Здесь мы совершенно не будем касаться этого вопроса, просто следует знать, что именно для работы со звуком важно иметь «запас прочности» — более высокую частоту дискретизации и разрядность.
Что же касается воспроизведения музыки, здесь также не обойтись без апсемплинга (повышения частоты дискретизации). То есть, фактически Sony DSEE HX — это и есть апсемплинг, который нужен для того, чтобы композиция, пройдя конвертацию из цифрового сигнала в аналоговый, содержала минимальное количество искажений.
Но проблема с DSEE HX состоит в том, что буквально все современные цифровые ЦАПы и без помощи сторонних алгоритмов автоматически повышают дискретизацию. То есть, эта функция сама по себе не имеет смысла.
За одним важным исключением — эффект плацебо. Стоит вам лишь активировать эту опцию и увидеть на экране смартфона загоревшуюся надпись DSEE HX, как звук «действительно» становится более прозрачным, кристально чистым и объемным. Хотя бы в вашем воображении.
P.S. Не забудьте подписаться в Telegram на наш научно-популярный сайт о мобильных технологиях, чтобы не пропустить самое интересное!
