Последний альбом группы Queen с участием легендарного Фредди Меркьюри был записан уже после смерти вокалиста. И в этом альбоме есть одна интереcная песня, собранная буквально по кусочкам из обрывков записей Меркьюри, сделанных незадолго до смерти.
Эта композиция не должна была появиться и никто в Queen даже не думал, что из этих обрывков что-то можно сделать. Но продюсер группы практически самолично собрал всё воедино и создал знаменитую… как же ее… Простите, но название совершенно вылетело из головы.
И что же делать в подобных ситуациях?
Раньше, услышав красивую песню где-нибудь в кафе или на улице, вы могли достать смартфон, запустить приложение Shazam или SoundHound и тут же получить всю подробную информацию. Но сегодня бурный рост технологий позволил нечто большее!
Возвращаясь к забытой песне Фредди Меркьюри, мне достаточно запустить на смартфоне Google Ассистент, сказать фразу «Что сейчас играет?», а затем просто напеть мелодию, которая крутится в голове — «та-да-та-тааааа та-та-та-таааа та-да-та-таааа»:
И буквально через несколько секунд смартфон выдает правильный результат — You Don’t Fool Me группы Queen:
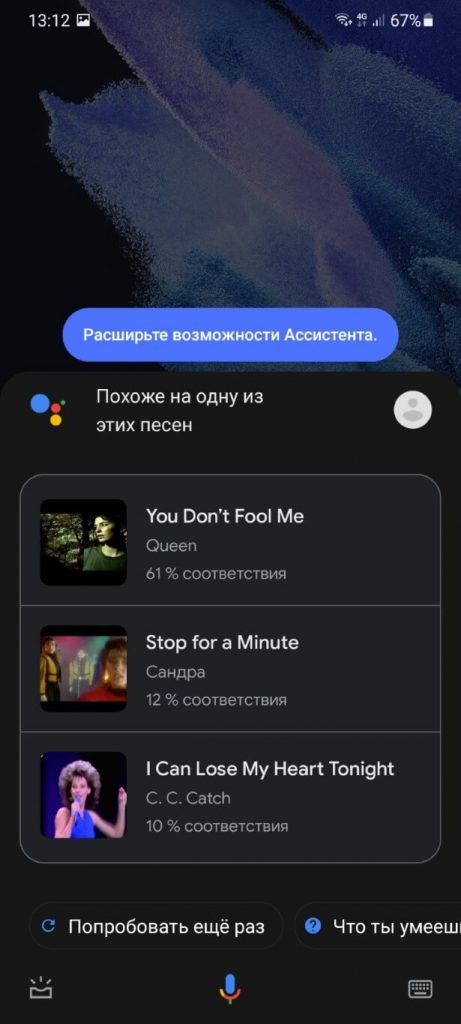
Как это вообще возможно!? Обычно в таких ситуациях отвечают — искусственный интеллект. Но если вам хочется получить настоящий ответ, тогда предлагаю вместе со мной погрузиться в увлекательный мир музыки!
После прочтения этой статьи вы поймете, как именно бездушный процессор смартфона стал еще на один шаг ближе к человеческому разуму. Или, по крайней мере, научился еще лучше его имитировать.
Часть 1. Природа звука
Бессмысленно говорить о том, как работает Shazam или распознавание музыки в целом, если не понимать, что такое музыка и звуки вообще. Поэтому вначале я уделю немного внимания этому вопросу.
Если же вы хорошо в этом разбираетесь, тогда переходите к следующему разделу. Но помните — понять работу Shazam без понимания этих основ будет тяжело.
Итак, звук возникает у нас в голове, когда воздух стучит по барабанной перепонке в наших ушах. Очень подробно этот процесс я описывал в статье о шумоподавлении или вреде громкой музыки. Так что здесь не будем повторяться.
Сам по себе воздух не может ни ударить по барабанной перепонке, ни сдвинуть с места даже пылинку. Это делают миллиарды молекул, хаотично летающих в пространстве.
Но чтобы они могли что-то или кого-то ударить, вначале нужно хорошенько их толкнуть — в точности как шары в бильярде. Именно это и делает любой динамик. Он движется вперед и назад, толкая молекулы воздуха то в одну, то в обратную сторону.
Мы даже можем отобразить это движение динамика на графике в виде волны:
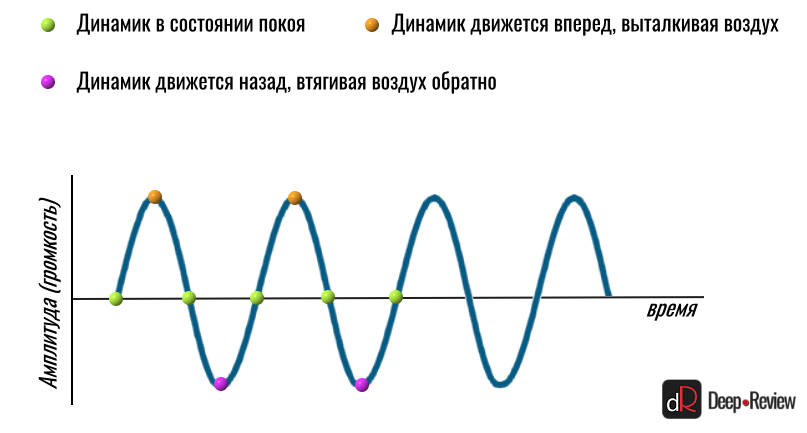
Чем сильнее динамик отклонится в сторону (или вверх/вниз на графике), тем выше будет волна, а значит звук — громче. То, какую ноту или звук мы услышим, зависит только от того, сколько движений вперед-назад за одну секунду сделает наш динамик.
Если за 1 секунду произойдет 440 движений вперед-назад, мы услышим ноту ля. И не важно, что будет вибрировать 440 раз в секунду — струна гитары, фортепиано или школьная линейка, прижатая одной стороной к столу — мы будем слышать ноту ля.
Вот только если это будет делать динамик, вместо приятного звука мы услышим не очень приятный монотонный гул:
Почему так происходит? Почему, когда мы нажимаем клавишу ля на пианино, она звучит приятно, а не так «искусственно», будто сгенерирована на компьютере?
Всё дело в том, что в реальном мире практически не существует идеальных движений. То есть, если бы струна гитары или скрипки вибрировала или двигалась вперед-назад только так:

Тогда бы мы услышали точно такой же монотонный неприятный гул, как в примере выше. Что более интересно, совершенно неважно, на каком инструменте мы пытались бы воспроизвести ноту ля (на фортепиано, скрипке, гитаре) — во всех случаях мы бы услышали один и тот же монотонный звук.
А теперь посмотрите в замедленном движении, что происходит со струной в реальности (на примере скрипки):

Такое движение скорее можно схематически изобразить вот так:

И это еще очень упрощенный пример. На самом деле, движение струны гораздо сложнее! Струна вибрирует вся целиком (как показано на первой анимации) и создает звук на частоте 440 Гц (монотонная нота ля). Но также вибрирует и каждая половинка струны, создавая звуки на частотах 880 Гц (половинка в два раза короче целой струны, а значит и вибрирует в 2 раза быстрее, т.е. 880 раз в секунду).
Кроме того, струна вибрирует третями, четвертями и т.д. И каждый участок струны, вибрируя, запускает еще отдельные звуковые волны на частотах в 3, 4, 5 (и так до бесконечности) раз выше основного тона (в нашем примере — нота ля или 440 Гц). Каждая такая вибрация создает свой собственный монотонный звук на более высоких частотах.
Мы называем такие звуки гармониками. То есть, основная гармоника — это частота 440 Гц (если мы говорим о ноте ля), вторая гармоника — это когда струна будет вибрировать половинами, т.е. звук на частоте 880 Гц, третья гармоника — 1320 Гц (440*3) и так далее.
А теперь добавьте к этому еще и вибрацию корпуса инструмента, например, скрипки. Ведь струна жестко закреплена на корпусе и ее вибрация также приводит к вибрации всего инструмента. Эти вибрации в свою очередь зависят от породы дерева, толщины корпуса и его формы.
Каждая такая вибрация добавляет к нашему ансамблю звуков еще и свои монотонные писки на разных частотах.
Именно эти дополнительные частоты/ноты/звуки, вызванные особенностями колебания струны/корпуса и создают уникальный тембр каждого музыкального инструмента.
Мы можем даже самостоятельно создать звук похожий на пианино или гитару, просто взяв монотонный гул, который я приводил выше, и добавить к нему еще различные монотонные пищалки, только на более высоких частотах и с разной громкостью.
От того, насколько громко (и как долго) будет звучать каждая дополнительная частота и зависит тембр инструмента.
Реальная звуковая волна
Вы наверняка не раз видели звуковую волну какого-то реального звука и она совершенно не похожа на все эти красивые графики волн, которые встречаются в статьях, например, такую:

В реальности звук «выглядит» скорее так:

Но как это понимать? Где здесь красивые привычные волны? Как хотя бы понять частоту этой звуковой волны? Напомню, частота — это количество волн за секунду. К примеру, на синем графике чуть выше мы видим частоту 8 Гц или 8 волн за секунду. А на втором графике вообще отсутствуют какие-то повторяющиеся узоры. Почему?
Ответ на этот вопрос уже дан чуть выше. Ни один инструмент не создает только одну звуковую волну на одной частоте. В этом случае мы бы слышали монотонный гул. Но так как на основной тон накладывается еще десяток-другой частот, график полностью искажается.
Вот, к примеру, у нас есть основная частота 440 Гц (нота ля):

Струна будет создавать другие частоты, первой из которых станет 880 Гц (это вторая гармоника или 440*2). Такая частота будет получаться, когда две половинки струны будут вибрировать отдельно. И выглядеть вторая волна (880 Гц) будет уже так:

То есть, мы видим, что количество волн увеличилось вдвое (440 Гц и 880 Гц). Но две волны не будут путешествовать по воздуху отдельно, они сольются в одну. И какой же она будет?
Какие-то пики одной волны совпадут с впадинами другой и немного погасятся, в каком-то месте пики двух волн наложатся и она станет еще выше (громче). В общем, вместо двух волн разной частоты мы получим одну волну такого вида:
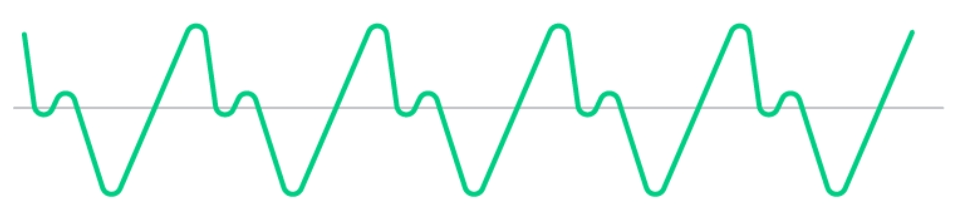
Глядя на эту волну, мы даже можем легко себе представить, как именно будет двигаться динамик, чтобы воспроизвести этот звук.
Вначале он максимально отклонится вперед, толкая молекулы на нас, затем назад до состояния покоя (прямая серая линия или 0 по оси Y — это состояние покоя), затем немножко вперед (маленький зеленый горбик на графике), после чего резко назад, втягивая воздух обратно (зеленая линия идет вниз, ниже серой полоски). Затем динамик снова вытолкнет весь воздух вперед (максимальная горка на графике) и так далее.
Естественно, чем больше разных частот будет создавать струна своим колебанием, тем сложнее окажется финальный «рисунок».
Таким образом, реальная звуковая волна — это результат наложения сотен волн различной частоты. Оттого она и выглядит так сложно.
На этом мы, пожалуй, и остановимся. Этих знаний должно хватить для понимания основной темы.
Часть 2. Как работает Shazam и любая другая технология распознавания музыки
Если я попрошу вас напеть какую-то музыкальную композицию, что именно вы споете? Будете ли вы учитывать басовую партию или партию ударных инструментов? А если речь идет об оркестровой музыке, в которой одновременно могут звучать десятки музыкальных инструментов?
Конечно же, вы просто напоете основную мелодию, игнорируя всё остальное. И что самое удивительное, я без проблем пойму, о чем идет речь. Даже если до вашего исполнения слушал эту композицию только на хорошей акустике в высоком качестве.
То есть, мы интуитивно можем сократить очень сложную и красивую музыку до нескольких простых нот. Точно так же работает и технология распознавания музыки. Вот только у смартфона нет интуиции и в этом его проблема.
Для бездушной железки даже самая прекрасная мелодия ничем не отличается от рёва мотора или простого шума ветра. Поэтому мы должны создать алгоритм, который бы привил смартфону чувство прекрасного. Этим и займемся!
Шаг 1. Анализируем частоты
Чтобы Shazam или любой другой сервис мог хоть что-то сделать с музыкой, он должен для начала ее «понять». То есть, вместо сложного и бессмысленного графика, вроде этого:

Наш смартфон должен увидеть, какие конкретно частоты звучат в каждый момент времени. Другими словами, он должен получить музыку в том виде, в котором она была до того, как все частоты смешались в один поток и направились к звукозаписывающей аппаратуре на студии.
К примеру, вместо сложной волны от нажатия клавиши фортепиано, в которой смешались монотонные звуки на частотах 440 Гц, 880 Гц и 1320 Гц, нам нужно получить эти частоты отдельно и узнать громкость каждой из них:
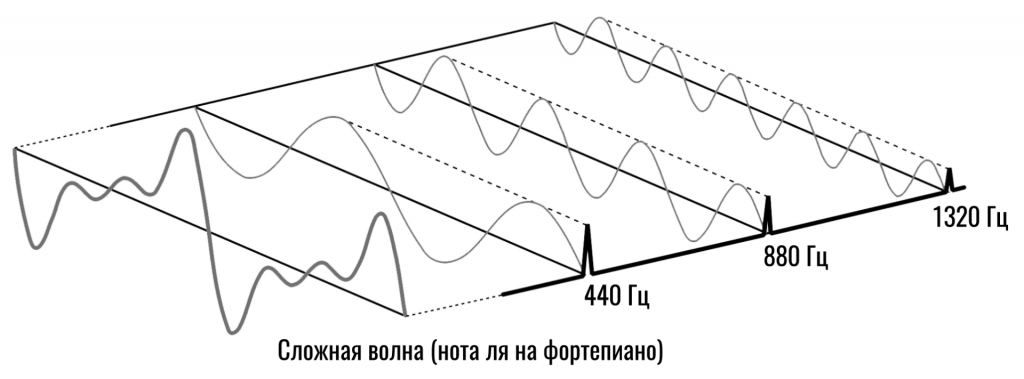
Это как если бы я показал вам цветное пятно и сказал, чтобы вы назвали, какие основные цвета и в какой пропорции я смешивал, чтобы получить этот уникальный цвет.
К счастью, нам не нужно ломать голову над этой задачей, так как ее успешно решил французский математик еще в 1807 году! Так появилась функция под названием преобразование Фурье.
При помощи этого математического метода мы получаем из сложной волны набор всех частот, из которых она состоит, а также амплитуду (громкость) каждой из них.
После этого у смартфона появляется спектрограмма. Это такой график, который по оси Y показывает конкретную частоту, а по оси X — время. То есть, мы можем видеть, какие частоты и насколько громко звучат в каждый момент времени:
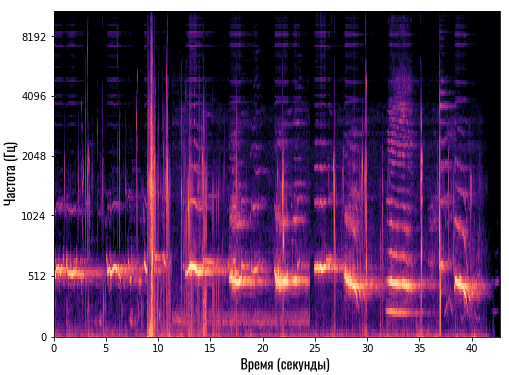
Так как у нас только две оси (X и Y), то громкость мы отображаем цветом. Чем ярче цвет — тем громче звучит эта частота.
К примеру, на спектрограмме выше мы видим, как где-то на 9-й секунде (по оси X) очень громко заиграли все инструменты или все частоты (красная вертикальная линия). А где-то на 31-й секунде частоты свыше 1500 Гц вообще пропали, то есть, в этот момент они не звучат в нашей композиции:
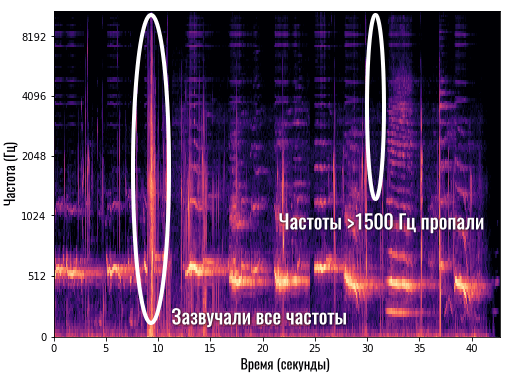
Согласитесь, в таком виде работать с музыкой гораздо проще и понятнее, чем смотреть на бессмысленный график ломаной линии. Здесь мы можем, к примеру, убрать какой-то дефект на частоте 10 000 Гц (какой-то лишний звонкий писк). Ведь мы увидим яркую полоску сверху, которую можно удалить, а затем снова сложить все частоты в один звук, но уже без удаленной частоты.
Теперь давайте подытожим. На первом шаге смартфон переводит записанный фрагмент мелодии в спектрограмму. Но пользоваться ею не получится. Ведь помимо мелодии, здесь присутствуют и посторонние звуки (шум улицы, кафе или разговоров, низкое качество микрофона и пр.).
Кроме того, в этой спектрограмме очень много информации. Смартфону она не нужна, как и нам не нужно знать все партии каждого инструмента, чтобы напеть фрагмент мелодии. И это приводит нас ко второму шагу.
Шаг 2. Создаем карту созвездий
Первое, что мы сделали для облегчения спектрограммы, это записали звук в режиме моно (стерео нам ни к чему), а также обрезали все частоты свыше 5000 Гц (или 4000 Гц — в зависимости от сервиса или алгоритма).
Естественно, качество звука сильно упало, так как мы слышим частоты до 15-20 тысяч герц (в зависимости от возраста) и эта информация есть в каждом музыкальном произведении. Но для распознавания музыки эти частоты совершенно не нужны. Основная мелодия находится гораздо ниже (в пределах 100-2000 Гц):

На этой картинке мы видим, что основной диапазон голосов и музыкальных инструментов (насыщенная темная часть каждой полоски) легко помещается до 1000 Гц, а уже гармоники уходят до предела слышимости.
А теперь начинается самое интересное! Алгоритм начинает анализировать полученную спектрограмму и искать на ней самые яркие области в каждый момент времени. Другими словами, он определяет, какие частоты (можем для простоты называть их нотами) звучат наиболее громко в конкретный момент времени.
Давайте возьмем нашу спектрограмму и отметим белыми точками такие «основные» частоты или ноты:
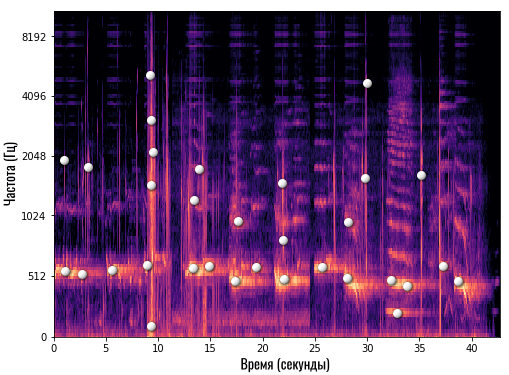
Сколько конкретно точек отмечает Shazam — сказать сложно, но это точно небольшое число (сравнительно). После такой обработки вместо массивной спектрограммы с большим количеством данных мы получаем очень компактную и аккуратную картину:
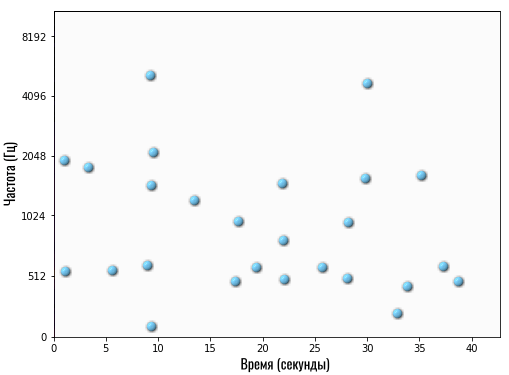
Теперь это своего рода уникальный отпечаток конкретной композиции. В Shazam его называют картой созвездий. Это примерно то, что делает наш мозг, когда мы хотим напеть сложную композицию — выделяет самые главные ноты.
Эта карта созвездий буквально показывает следующее:
- На 1-й секунде самые громкие частоты — это 512 и 2048 Гц
- На 5-й секунде самая ярко выраженная частота — 512 Гц
- На 30-й секунде композиции наиболее выражены частоты 1800 Гц и 4100 Гц
- И так далее
Помимо того, что мы колоссально сократили размер композиции, этот процесс естественным образом удалил все лишние звуки, так как на записи именно основная мелодия будет наиболее ярко выражена. Также мы удалили все гармоники, так как они практически всегда звучат тише основного тона.
Такую карту приложение создает на смартфоне еще до отправки данных на сервер Shazam. То есть, смартфон не передает звук.
В свою очередь компания также не хранит миллионы музыкальных композиций на своих серверах для сверки данных. Она пропустила каждую песню через этот алгоритм, чтобы получить ее «отпечатки». Они-то и хранятся на серверах.
Точнее, не совсем они…
Шаг 3. Убиваем главного врага — время
На данном этапе мы столкнулись с довольно серьезной проблемой. Предположим, вот это карта созвездий полноценной композиции на сервере Shazam:

Но человек даже теоретически не сможет каждый раз начинать записывать фрагмент интересующей его музыки с самого начала. Он может записать маленький кусочек где-то в середине композиции или за несколько секунд до конца песни.
В итоге, на смартфоне появится вот такая карта:
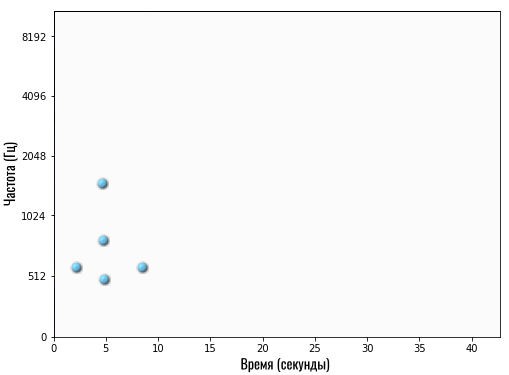
Если вы внимательно посмотрите, то увидите, что это фрагмент той же песни, что показана на карте чуть выше. Только в оригинале эти частоты (ноты) встречаются примерно с 19-й по 26-ю секунды, а здесь — примерно со 2-й по 9-ю.
Получается, смартфон передает серверу, что он услышал композицию, у которой на 5-й секунде ярко выражены 3 частоты: 510 Гц, 800 Гц и 1600 Гц (на графике по оси Y указаны только несколько частот, поэтому я называю частоты примерно).
Если сервер начнет искать у себя в базе данных композицию, у которой на 5-й секунде встречаются такие же основные частоты, то он может выдать любой результат, но только не правильный. Так как в оригинале эти частоты встречаются примерно на 22-й секунде.
А если не искать частоты с привязкой ко времени, то среди нескольких миллионов композиций может найтись сотня таких, в которых просто где-то встречаются 3 указанные частоты.
Что же делать?
Нужно избавиться от привязки ко времени, сохранив при этом привязку ко времени! Хотя это и кажется нелогичным на первый взгляд, решение получилось весьма элегантным.
Вместо списка частот (нот) с привязкой к конкретной секунде, мы берем одну любую точку на карте и связываем ее с несколькими другими точками. Например:
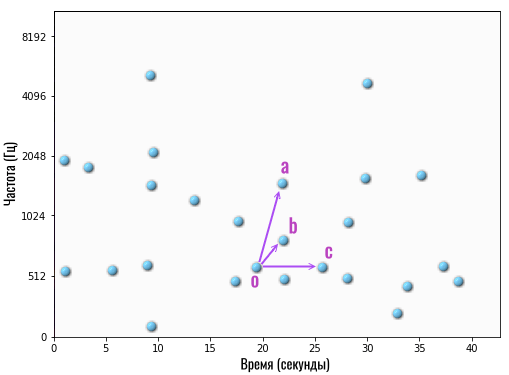
То есть, мы взяли опорную (главную) точку O (на 19-й секунде) и связали ее с несколькими другими точками (частотами/нотами) — a, b и c.
Под словом «связали» я лишь подразумеваю следующее. Мы берем две частоты и разницу во времени между ними. То есть, если мы говорим о связи O->A, тогда это две частоты: 515 Гц (точка O) и 1600 Гц (точка A), а разница во времени между ними составляет 3 секунды (точка A на 22 секунде минус точка O на 19 секунде).
Вот и всё! То есть, вместо конкретных частот с привязкой к определенному времени, мы храним информацию о том, как связаны конкретные частоты между собой. Например, сохраняем информацию о том, что в определенной композиции звук на частоте 1600 Гц начинается спустя 3 секунды после звука на частоте 515 Гц.
Теперь мы можем передать эту информацию на сервер и он поищет, есть ли у него в базе такая мелодия, в которой прозвучала частота 515 Гц, а затем ровно через 3 секунды был звук на частоте 1600 Гц.
Конечно, мы передаем не одну «связку частот», а множество. И какие-то пары будут встречаться в разных композициях, особенно если это ремикс популярной песни. Но Shazam или любой другой сервис выдаст в качестве результата ту песню, в которой таких совпадений было больше всего.
Размышления вместо выводов
Только что мы рассмотрели базовый принцип работы любого сервиса по распознаванию музыки. Конечно, у вас могло остаться множество вопросов, так как я хотел раскрыть тему в общих чертах, чтобы она была понятной самому широкому кругу читателей.
Например, не совсем понятно, по какому принципу алгоритм выбирает опорные точки, от которых затем строит связи с другими частотами.
Ответа на этот вопрос у меня нет, так как Shazam не раскрывает свои алгоритмы в таких деталях. Возможно, компания выбирает для каждого момента времени первую по счету точку (счет ведется снизу вверх слева направо) и связывает ее с несколькими рядом стоящими точками.
Кроме того, я не рассказал о том, как именно передаются и хранятся такие записи. Для этого используются хеши. Но само понятие хеш-функции настолько интересное и важное, что мне не хотелось использовать его без подробного и понятного объяснения. А это бы заняло еще больше места в статье и усложнило восприятие информации.
Также мы коснулись только алгоритмов, без упоминания нейросетей. А именно последние используются Google Ассистентом для определения мелодии, когда человек просто напевает или насвистывает мотив песни.
В этом случае также создаются уникальные «отпечатки» каждой песни, только затем добавляется еще один важный этап. Когда Google создала базу «отпечатков», для каждой такой песни были собраны «отпечатки» простых мелодий, напетых обычными людьми.
Затем нейросеть обучили находить оригинал по плохому неточному отпечатку, полученному с напетой человеком мелодии. Когда нейросеть прошла обучение на тысячах примеров, теперь она способна самостоятельно сопоставлять отпечаток напетой мелодии с отпечатком оригинала на серверах Google.
Более подробно о том, как работают нейросети и что такое обучение нейросетей, мы рассказывали в отдельной статье.
Алексей, глав. ред. Deep-Review
P.S. Не забудьте подписаться в Telegram на наш научно-популярный сайт о мобильных технологиях, чтобы не пропустить самое интересное!
