Биннинг пикселей «для чайников». Работает ли эта технология на смартфонах?

Биннинг пикселей — это объединение нескольких маленьких пикселей в один крупный с целью улучшить качество изображения.

Подобная технология появилась не вчера и даже не 10 лет назад, но в мобильной фотографии биннинг стал сверхпопулярным буквально пару лет назад — в тот самым момент, когда на рынке стали появляться доступные камерофоны с 48-Мп камерами. Производители так увлеклись этой технологией, что только за один 2019 год прошли путь от 12 до 108 мегапикселей!

Сегодня практически все флагманские камерофоны используют биннинг, объединяя в группы по 4 и даже 9 пикселей. Но зачем? Есть ли в этом какой-то практический смысл или это очередной маркетинговый инструмент?

Основная проблема заключается в том, что мобильные матрицы не увеличиваются пропорционально росту их разрешения, а значит, приходится сокращать размер каждого пикселя.

В 2019 году мы начали с 800-нанометровых пикселей (0.8 мкм), размер которых вплотную подошел к длине волны красного света. А совсем недавно Samsung представила первый 200-Мп сенсор с пикселями 640 нм! То есть, размер пикселя стал де-факто меньше длины волны красного света (625 — 740 нанометров).

Следовательно, ни один мобильный объектив физически не способен сфокусировать точку красного цвета, которая бы «помещалась» в такой маленький пиксель¹, если, конечно, не учитывать физическое объединения нескольких пикселей под одним цветным фильтром.

Получается, даже теоретически новый сенсор не способен разрешить детали красного цвета. И вопрос о том, нужно ли такое разрешение, приобретает новый смысл.

Но это тема для другого разговора. Сейчас же важно понять, есть ли какой-то толк от объединения четырех или девяти 0.8-мкм пикселей в один, размером 1.6 или 2.4 микрометра. Ведь именно такие конфигурации сегодня встречаются чаще всего.

Введение в курс дела. Или о чем вообще разговор?

Как вы знаете, матрица любой цифровой камеры, будь-то зеркальный фотоаппарат или смартфон, не способна различать цвета. Пиксель (кусочек кремния) умеет только улавливать количество света (яркость) безотносительно к его цвету.

Чтобы получить цветное изображение, мы разделяем все пиксели на 3 группы — одни будут игнорировать весь свет, кроме красных оттенков, другие будут воспринимать только зеленые тона, а третьи — синий свет.

Для этого мы просто над каждым пикселем размещаем цветное стеклышко, которое и будет пропускать только свой цвет. В итоге, кусок кремния под красным фильтром будет фиксировать количество только «красных» фотонов из общего потока и так далее:

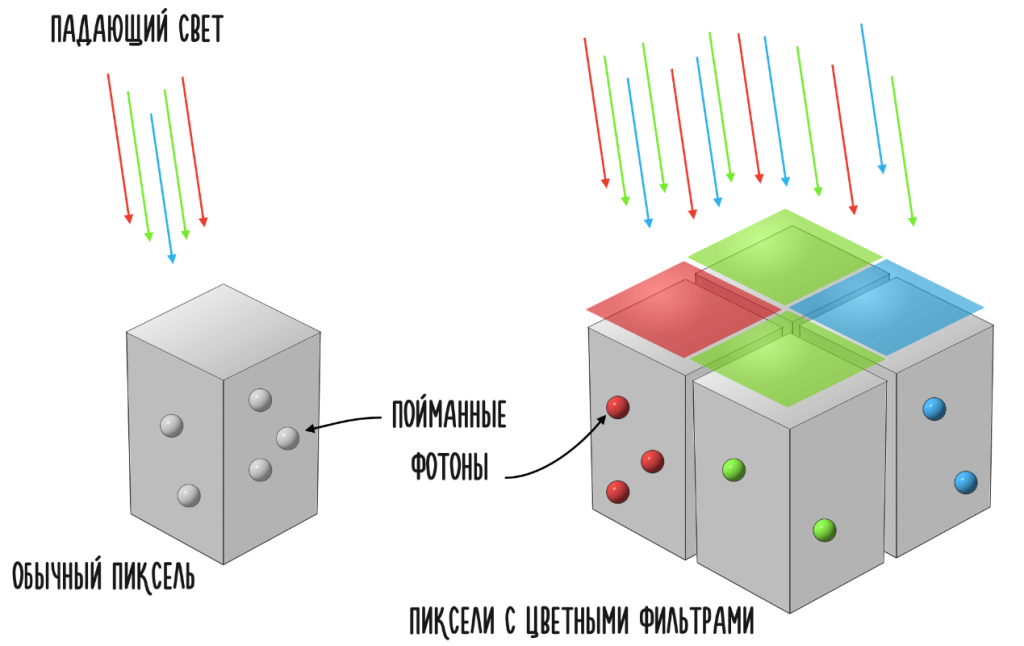
Именно так устроены пиксели на матрице любой камеры, кроме современных — тех, что используют биннинг. Эти матрицы спроектированы немного по-другому.

Если производитель заявляет о 48 мегапикселях, то на такой матрице действительно используется 48 миллионов физических пикселей (кусочков светочувствительного кремния). Однако все они собраны в группы по 4 пикселя, которые накрыты одним цветным фильтром:

Но зачем такие сложности? Почему бы просто не разместить 48 миллионов крохотных пикселей, каждый со своим отдельным маленьким цветным фильтром?

Сделано это для того, чтобы при необходимости 48-Мп матрица «превращалась» в 12 мегапикселей. То есть, чтобы 4 пикселя под одним цветным фильтром работали как один более крупный пиксель одного цвета.

А когда в этом нет нужды, каждый пиксель может работать отдельно, выдавая фото с более высокой детализацией:

Получается, пиксели на современных матрицах могут изменять свой размер при необходимости от 0.8 мкм до 1.6 или даже 2.4 мкм, в зависимости от типа биннинга.

Но всё это лишь красивая теория, а как обстоят дела в реальности? Может ли биннинг реально улучшить качество снимков? Действительно ли группа маленьких пикселей ведет себя так, как один большой?

Ответить на этот вопрос невозможно, если не понимать, в чем, собственно, преимущество больших пикселей перед маленькими. Мы должны чётко осознавать, каким образом сам размер пикселя влияет на качество фотографии. И только потом можно разбираться, действительно ли биннинг увеличивает размер пикселя.

Почему один большой пиксель лучше одного маленького? Или поговорим о случайностях

Давайте представим, что у нас есть идеальный профессиональный фотоаппарат. Под словом идеальный я подразумеваю, что все пиксели этой камеры без малейших искажений фиксируют каждый падающий фотон света, затем все фотоны подсчитываются и их количество оцифровывается с максимальной точностью.

Будет ли такая камера всегда выдавать снимки превосходного качества? К сожалению, нет. Качество фотографий в этом случае будет полностью зависеть от количества света, которое захватит фотоаппарат.

И проблема не в том, что при недостаточном освещении снимки будут просто темноватыми, а при хорошем — яркими. Несмотря на безупречное качество нашей идеальной камеры, при плохом освещении она будет выдавать грязные фотографии с огромным количеством шума.

Вот пример сцены, снятой на «идеальную камеру» с разным уровнем освещенности. Слева показан снимок, на каждый пиксель которого в среднем падало по 10 фотонов, а справа — 1000 фотонов:

Откуда же взялась эта «грязь» на фотографии слева? Почему при недостаточном освещении идеальная камера выдала столько шума вместо того, чтобы просто выдать более тёмную копию той фотографии, что показана справа?

Проблема заключается в самой природе света. Когда его становится слишком мало (например, мы сократили время выдержки или вокруг просто недостаточно света), фотоны начинают «играть в кости», выбрасывая каждый раз случайный результат.

Сколько бы раз мы ни пытались сделать снимок в условиях плохой освещенности, мы всегда будем получать разный результат.

К примеру, если мы сделаем 5 снимков чисто белой стены, то один и тот же пиксель каждый раз будет фиксировать разное количество фотонов. Скажем, во время первого снимка на него упадет 10 фотонов, второго — 12, третьего — 8 и так далее.

В результате, одна и та же точка одного и того же предмета на каждом снимке будет отличаться. И чем меньше было света, тем сильнее это различие. Более того, даже на одном снимке яркость всех точек одинаково белой стены будет также отличаться, ведь на соседние пиксели упадет разное количество фотонов.

Именно это мы и увидели на фото выше. Там, где пиксели неба должны были быть одного цвета, на «грязном» снимке яркость каждой конкретной точки сильно отличалась от яркости соседней.

Что такое шум и откуда он берется?

На самом деле, никакой мистики в этом нет. Падение фотонов на матрицу (или на каждый конкретный пиксель) — это такое же случайное событие, как и падение капель дождя на тротуарную плитку.

Когда идет моросящий дождик с низкой интенсивностью, на каждую плитку упадет совершенно разное количество капель. И чем реже падают капли, тем сильнее будет отличаться их общее количество на плитках.

Так и со светом. От белой стены на один пиксель может прилететь 10 фотонов, на другой — 12, а на третий — 8. Но чтобы стена на снимке выглядела такой же чисто белой, как и в жизни, на каждый пиксель должно упасть одинаковое количество фотонов.

Если на конкретный пиксель попало 8 фотонов, это значит, что погрешность составила -2 фотона, так как в идеале мы ожидали увидеть здесь 10 фотонов. Если на второй пиксель попало 12 фотонов, то погрешность составила +2 фотона и т.д.

Это естественное отклонение количества упавших фотонов от ожидаемого и называется шумом (более точно — фотонным или дробовым шумом). Чем это отклонение сильнее, тем сильнее будет отличаться и яркость соответствующей точки на снимке.

Но как же нам определить уровень шума?

Для этого достаточно выполнить простую инструкцию:

1. Сделать 3 снимка подряд и посмотреть, сколько фотонов упало на конкретный пиксель в каждом снимке.
2. Посчитать среднее количество фотонов, падающее каждый раз на один и тот же пиксель.
3. Определить, как сильно количество фотонов каждый раз отличалось от среднего значения.
4. Сложить эти отличия и разделить на 3, так как мы проводили эксперимент 3 раза.

Чтобы всё стало предельно ясно, рассмотрим простой пример.

Пример

Если первый раз на пиксель упало 8 фотонов, второй — 10, а третий — 12, тогда в среднем на пиксель падало 10 фотонов, так как (8+10+12)/3 = 10.

Теперь нам нужно понять, насколько отличается количество фотонов, падающее на пиксель каждый раз, от среднего значения. Если первый раз на пиксель упало 8 фотонов, а среднее значение равняется 10, тогда мы получим 8-10=-2.

Соответственно, количество фотонов, упавших на пиксель в первый раз, отличается от среднего значения на -2, во второй раз — на 0 (так как 10 — это и есть среднее количество фотонов), а последний раз — на +2, так как 12-10=2.

Осталось сложить все эти отклонения и разделить на 3. Так мы и узнаем средний разброс значений или шум:

(-2+0+2)/3=0

Ноль!? Получается, что в среднем разброса количества фотонов и не было вовсе!? Но это же, очевидно, противоречит нашему наблюдению.

Конечно, мы допустили логическую ошибку, ведь количество фотонов отличалось как в положительную, так и отрицательную сторону. Сложив эти отклонения, мы их компенсировали, то есть, пришли к нулю.

Как же нам выйти из этой ситуации? Нужно избавиться от отрицательных чисел, для чего достаточно просто возвести их в квадрат. Пробуем:

(-2)²+0²+2²=4+0+4=8, теперь делим 8 на 3 и получаем 2.7.

Вот оно! Средний уровень шума составил 2.7 фотона, то есть, количество фотонов (а значит и яркость каждой точки) в среднем отличается на 2.7. Верно? И снова, нет!

Полученное нами число — это важнейший показатель в статистике, который называется дисперсией. Дисперсия показывает, как сильно разбросаны значения случайных величин или событий.

И это практически то, что нам нужно, за одним серьезным исключением — мы же возводили все значения отклонений в квадрат. То есть, дисперсия показывает среднее отклонение значений от среднего, возведенное в квадрат.

Чтобы узнать реальное отклонение значений от среднего (в статистике это называется стандартным отклонением), нужно избавиться от квадрата, для чего достаточно просто взять квадратный корень из дисперсии:

Стандартное отклонение = √2.7 = 1.64

Вот мы и получили заветную цифру! Это и есть уровень шума или то, насколько в среднем количество фотонов в конкретном пикселе отличается от ожидаемого или среднего.

Отношение сигнал/шум как важнейший показатель качества

Итак, представьте, что на конкретный пиксель нашей мобильной матрицы падает в среднем 10 фотонов. Как узнать уровень шума для этого пикселя при таком количестве фотонов? Неужели нам нужно что-то подсчитывать, суммировать, возводить в квадрат, а затем брать квадратный корень!?

К счастью, ничего этого делать не нужно. Дело в том, что дождь, подбрасывание монетки, падение фотонов или количество звонков в колл-центр — это особый вид случайных событий, который описывается так называемым законом Пуассона (или распределением Пуассона).

Если наступившее событие никак не влияет на наступление следующего события и все события происходят с определенной частотой, тогда они распределяются по закону Пуассона².

А если так, тогда согласно распределению Пуассона, дисперсия — это и есть среднее значение.

В нашем предыдущем примере на один пиксель в среднем падало 10 фотонов. Так как в реальной жизни (а не рассмотренном нами примере) падение фотонов распределяется по закону Пуассона, нам не нужно определять дисперсию, высчитывая все отклонения от среднего, суммируя их квадраты и пр. Число 10 — это уже и среднее значение, и дисперсия одновременно по определению.

Другими словами, если какие-то случайные события распределяются по закону Пуассона, тогда мы можем посчитать средний результат, а затем найти среднее отклонение всех его значений в квадрате и мы получим то же число. То есть, среднее значение будет равняться дисперсии. Поэтому высчитывать её отдельно не нужно.

В таком случае, чтобы узнать уровень шума (посчитать стандартное или реальное отклонение), нам нужно просто взять квадратный корень из числа 10 (из дисперсии).

Это и есть основное правило, которое описывает количество фотонного шума в пикселях.

Если на пиксель в среднем падает по 100 фотонов, уровень шума будет √100 или 10 фотонов, если падает в среднем 1000 фотонов, уровень шума будет √1000 или 31 фотон. Так как, повторюсь, среднее количество фотонов при распределении Пуассона — это и есть дисперсия (среднее отклонение всех значений в квадрате).

Отсюда мы приходим к важнейшему показателю качества изображения — отношению сигнала к шуму (SNR).

Если на один пиксель в среднем падает 10 фотонов, шум будет равняться √10 или ~3 фотона. Тогда отношение сигнал/шум или SNR для такого пикселя будет составлять 10/3 = 3.33. То есть, уровень сигнала (10 фотонов) отличается от бесполезной информации или шума (3 фотона) всего в ~3 раза и это очень плохо.

Увидеть такой шум на глаз — проще простого, ведь яркость пикселей, которая должна была быть идентичной (как в случае с белой стеной), на фото будет отличаться на треть (100% разделить на SNR).

Если же, скажем, количество фотонов будет 1000, а шум — 31 фотон (√1000), тогда SNR=1000/31=32, то есть, полезный сигнал отличается от бесполезного (шума) в 32 раза! Соответственно, яркость пикселей, которая должна была быть идентичной, в реальности будет отличаться всего на 3% (100%/32=3%)!

Когда света становится очень много и на каждый пиксель падает огромное количество фотонов, скажем, 50000, тогда заметить фотонный шум вообще невозможно. Ведь шум из 50 тыс. фотонов — это 223 фотона, соответственно SNR=223, а значит, яркость каждой точки будет отличаться не более, чем на 0.4% (при оцифровке сигнала такая разница, скорее всего, буде вообще проигнорирована и яркость пикселей не будет отличаться вовсе).

Когда на тротуарную плитку упало несколько капель дождя, какой-то участок плитки будет более сухим, а где-то будет больше воды. Но когда идет ливень, вся плитка будет одинаково залита водой и увидеть какое-то различие невозможно.

Почему большой пиксель лучше маленького в плане SNR?

Думаю, вы уже прекрасно понимаете, что на более крупный пиксель упадет больше фотонов, соответственно, его сигнал/шум будет выше.

Если на 4 маленьких пикселя падает по 25 фотонов, то, будь на их месте один большой пиксель, на него бы упало 100 фотонов:

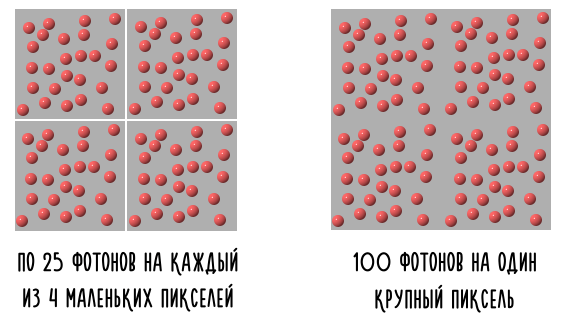
Мы можем легко посчитать SNR каждого пикселя:

• SNR маленького пикселя. Так как на маленький пиксель упало 25 фотонов, то шум составил √25 или 5 фотонов, значит, SNR=5.
• SNR большого пикселя. На большой пиксель упало 100 фотонов, шум составил √100 или 10 фотонов. Соответственно, SNR=10.

Получается, если площадь крупного пикселя в 4 раза больше маленького, то его SNR будет в 2 раза выше.

Поэтому при недостаточном освещении мы можем делать снимок чище за счет увеличения размеров пикселей на матрице, чтобы на каждый из них падало больше фотонов.

Работает ли на смартфонах биннинг пикселей?

Теперь мы можем ответить на главный вопрос — действительно ли «программное» объединение пикселей увеличивает их SNR или сигнал/шум.

Почему программное? Потому что физически на матрице 4 пикселя не «склеиваются» в один большой. Это всё те же 4 маленьких физических пикселя, с которых смартфон считывает небольшой сигнал и программно объединяет его, увеличивая в 4 раза.

Логика подсказывает, что это должно работать в идеальной камере. То есть, нет никакой разницы, сколько пикселей размещено на площади, скажем, 2.4×2.4 мкм. Если на этот участок сенсора падает 540 фотонов, они упадут сюда в любом случае, будь там 1 большой пиксель (2.4 мкм) или 9 маленьких (0.8 мкм).

Вы можете подумать, что 9 маленьких пикселей не занимают в реальности всей площади одного большого, ведь между пикселями есть перегородки, а внутри, помимо светочувствительного кремния, размещена и другая электроника (транзисторы, конденсаторы и пр.).

Поэтому, может показаться, что маленькие пиксели в группе менее эффективны, чем 1 большой:

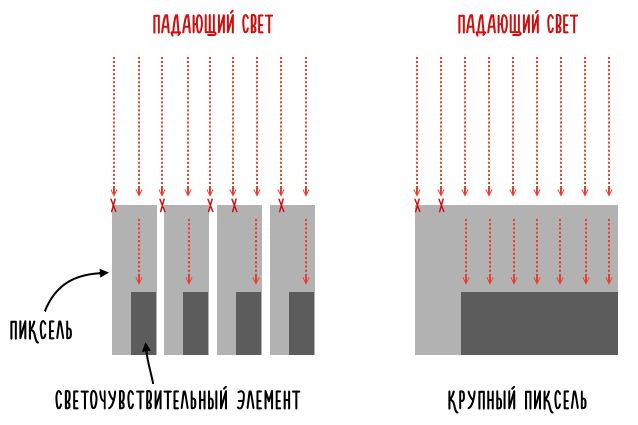
Но в реальности это не так. Чтобы исключить подобную проблему, все пиксели накрываются микролинзами, которые нужным образом перенаправляют падающий мимо светочувствительного элемента (фотодиода) свет, чтобы ничего не потерялось по пути:

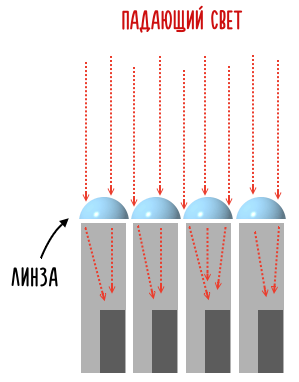
Поэтому, когда камера смартфона применяет биннинг, практически нет никакой разницы, находится ли на матрице один крупный пиксель или, скажем, 9 маленьких. В первом случае камера просто считывает 540 фотонов и получает фотонный шум 23 фотона (√540). Во втором случае камера считывает в среднем по 60 фотонов с 9 маленьких пикселей, шум которых равняется 8 фотонам (√60).

Затем при биннинге складывается как сигнал (60*9), так и шум √(60*9), в результате чего получаем те же сигнал 540 и шум 23 фотона, что и в случае с большим пикселем. А значит, SNR большого пикселя равен SNR группе из нескольких маленьких пикселей.

Получается, биннинг реально работает? Да, только с одним но…

У нас нет идеальной камеры!

До этого мы говорили только о гипотетической камере, которая не вносит никаких искажений в сигнал. Сколько фотонов упало, столько и оцифровали. Но в реальном мире сигнал, проходя по пути от фотона до точки на фото, искажается множество раз.

Прежде всего, электроника камеры вообще не имеет никакого дела с фотонами. Мы не собираем фотоны на матрице, не подсчитываем и не оцифровываем их.

Когда фотон падает на кусочек кремния, он может «раствориться» в нём, выбив электрон из атома кремния (фотодиода). А может и не выбить. Это первое, что следует учитывать при расчете SNR (в «идеальной камере» фотон всегда выбивал электрон).

Затем мы собираем электроны, высвободившиеся в результате фотоэффекта³. Но периодически в нашем кусочке кремния высвобождаются электроны и без участия фотонов. То есть, фотон не прилетел, а электрон всё равно появился. Связано это с нагревом матрицы, так как электрон может возбудиться от тепловой энергии и самостоятельно оторваться от атома.

Как нам отличить электрон, который появился из-за упавшего фотона, от электрона, который вырвался сам? Естественно, никак. Поэтому при расчете SNR нужно учитывать тепловой шум (случайное количество электронов от так называемого темнового тока⁴ или тепла).

Дальше мы считываем напряжение, образованное электронами и в конце оцифровываем его. Но представьте, сколько должно стоить оборудование, способное считывать напряжение с точностью до заряда одного электрона?

Поэтому сам процесс считывания вносит искажение в сигнал и это дополнительный шум, который нужно учитывать при расчете SNR пикселя.

Если мы хотим увидеть более реалистичный прирост качества сигнала, который дает биннинг в современных матрицах, нам нужно модифицировать нашу формулу, которая выглядела так:

SNR=фотоны / √фотоны

Когда 100 фотонов попадало в идеальную камеру, мы рассчитывали SNR, делив 100 (сигнал) на √100 (шум) и получали SNR=10. Но в неидеальном мире нужно учитывать дополнительный шум:

SNR=(фотоны * квантовую_эффективность) / √(фотоны + темновой_ток * время_выдержки + шум_считывания²)

Не пугайтесь этой формулы, её можно упростить.

Так как речь идет о камере смартфона, можно выбросить из этого уравнения темновой_ток * время_выдержки, так как тепловой шум является проблемой в астрофотографии, где используются очень длинные выдержки (от 2 минут и больше). На смартфонах выдержка редко превышает 1 секунду, поэтому в мобильной матрице электроны не отрываются от атомов из-за температуры.

Квантовая эффективность — это процент фотонов, которые упали на пиксель и выбили электрон. Если квантовая эффективность пикселя равняется 80%, тогда нужно количество упавших фотонов умножить на 0.8. Но мы можем также выбросить эту переменную, так как она не имеет отношения к теме нашего разговора, ведь квантовая эффективность не зависит от размера пикселя.

После всех упрощений наша формула будет выглядеть так:

SNR=фотоны / √(фотоны + шум_считывания²)

Вот здесь-то мы и видим основное ограничение биннинга. Один крупный пиксель не равен по SNR нескольким маленьким, так как при считывании сигнала с каждого маленького пикселя мы вносим шум считывания.

Поэтому, сигнал/шум одного большого пикселя будет отличаться от SNR четырех маленьких пикселей на тот самый шум считывания, так как до объединения пикселей мы считываем сигнал с маленьких пикселей 4 раза.

Чтобы окончательно разобраться в этой разнице, давайте рассмотрим простой пример. Представьте, что на площадь 1.6*1.6 (мкм) падает 200 фотонов, при этом шум считывания пикселей равен 2 электронам. То есть, если 200 фотонов выбили 200 электронов, то электроника может считать 198 или 202 электрона.

Теперь сравним сигнал/шум в разных сценариях:

SNR большого пикселя (матрица состоит из относительно крупных пикселей 1.6 мкм)

Так как всю площадь 1.6×1.6 мкм занимает один пиксель, то все 200 фотонов падают именно на него. Нам остается считать эту информацию, внеся 1 раз шум считывания (2 электрона). Вычислим SNR этого пикселя:

• SNR=200/√(200+2²)=200/√204=200/14.28=14

SNR маленького пикселя (матрица состоит из крохотных 0.8-мкм пикселей без биннинга)

Так как на площади 1.6х1.6 мкм располагается 4 маленьких пикселя, то на каждый конкретный пиксель упадет по 50 фотонов (200/4). Чтобы узнать сигнал/шум одного маленького пикселя остается лишь считать с него информацию, внеся 1 раз шум считывания:

• SNR=50/√(50+2²)=50/√54=50/7.23=6.8

SNR «увеличенного» пикселя после биннинга

Если наша матрица поддерживает биннинг, тогда нам нужно суммировать все фотоны с четырех маленьких пикселей, но для этого придется 4 раза считывать информацию, внося 4 раза шум считывания. Поэтому сигнал/шум «виртуального» большого пикселя будет составлять:

• SNR=4*50/√(4*50+4*2²)=200/√216=200/14.7=13.6

Из этого примера мы видим, что качество сигнала большого пикселя в 2 раза выше качества сигнала маленького. Однако при биннинге маленьких пикселей, даже с учетом вносимого шума считывания, качество сигнала «объединенного пикселя» практически не отличается от SNR физически большого пикселя.

Конечно, это при условии, что шум считывания равняется двум электронам. Какой он в действительности — не знает никто, так как производители смартфонов не раскрывают этой информации.

Шум чтения в крупных пикселях зеркальных фотоаппаратов может варьироваться от 1.5 электрона до 5, а иногда и выше. Но стоит учитывать, что зачастую шум считывания тем меньше, чем меньше сам пиксель.

Вместо выводов

К сожалению, эта статья не дает ответов на многие вопросы. В частности, мы рассматривали биннинг пикселей только в контексте плохого освещения, когда фотонов очень мало. А что будет при хорошем освещении?

Еще более важный вопрос заключается в том, что лучше — матрица с большими пикселями или несколькими маленькими? Помогает ли биннинг увеличить динамический диапазон камеры при хорошем освещении?

Обо всём этом мы поговорим как-нибудь в другой раз, но на главный вопрос, надеюсь, эта статья дала исчерпывающий ответ.

Биннинг пикселей — это не маркетинговая уловка, а реально работающий инструмент, который снижает количество шума и в целом улучшает качество снимков, оставляя при этом возможность снимать с более высоким разрешением, когда это уместно.

Понимая, как работает биннинг, вы можете использовать еще более простое правило. Если матрица объединяет пиксели 2×2, значит, это улучшает SNR (отношение сигнала к шуму) «склеенного» пикселя в 2 раза, если речь идет о биннинге 3×3, значит SNR увеличивается в 3 раза и т.д.

Разумеется, при биннинге разрешение снимков падает пропорционально. Увеличивая SNR в 2 раза, мы сокращаем разрешение в 4 раза (2²), если хотим увеличить сигнал/шум в 3 раза, разрешение упадет в 9 раз (3²) и т.д.

Соответственно, 48 Мп камера с биннингом 2×2 выдает 12-Мп снимки (48/2²), у которых SNR выше в 2 раза, а 108 Мп камера при бининге 3×3 выдает 12-Мп снимки (108/3²), у которых SNR выше в 3 раза.

Иногда встречаются ситуации, когда смартфон не способен выдавать снимки в полном разрешении. У нас частенько бывали такие аппараты на обзорах.

К примеру, 48-Мп камера какого-то смартфона всегда выдает только 12-Мп снимки, полученные при биннинге. Если же пользователь выбирает в настройках полное разрешение, то смартфон всё равно делает 12-Мп снимок с биннингом, а затем просто растягивает картинку в 4 раза. В этом, естественно, нет никакого смысла.

Но тогда может возникнуть другой вопрос — в чем, собственно, сложность снимать в полном разрешении? Почему некоторые смартфоны всегда выдают результат в биннинге, если они в любом случае считывают каждый отдельный пиксель и только потом «склеивают» их в группы?

Ответ заключается в цветных фильтрах. Если вы посмотрите на картинки в начале статьи, то заметите, что пиксели группируются под фильтром одного цвета. Соответственно, чтобы восстановить исходный цвет, гораздо проще «склеить» группу пикселей в один, так как они уже накрыты одним цветом.

Если же попытаться восстановить полное разрешение, то есть, цвет каждого отдельного пикселя, нужно использовать гораздо более сложный и требовательный к вычислительным ресурсам алгоритм. Тема дебайеризации (восстановления цвета) выходит за рамки этой статьи, но просто знайте, что чем больше пикселей «накрыты» одним цветом, тем сложнее восстановить исходный цвет.

Поэтому в дешевых смартфонах никто даже не пытается этого делать и маленькие пиксели одного цвета просто складываются в один «большой пиксель».

Алексей, главред Deep-Review