Один из читателей DR как-то задал очень простой и конкретный вопрос — каким образом миллиарды микроскопических переключателей (они же — транзисторы) делают так, чтобы на экране смартфона появлялось изображение, а из динамика играла музыка?
Действительно, как это происходит? Ведь внутри телефона нет никакого разума или интеллекта. И, всё же, эти устройства достаточно умны.
К большому сожалению, простого ответа на этот вопрос нет и нам потребуется больше времени, чтобы лишь немножко приоткрыть завесу тайны.
В первой части мы выяснили, что для смартфона не существует никакой музыки, фильмов, фотографий, книг или приложений. Он оперирует лишь единичками и ноликами. Также мы разобрались, как именно картинка, текст или другая информация превращаются в те самые единички и нули, которые затем сохраняются в памяти смартфона.
Но постойте-ка! Какие ещё единички и нули, какая память!? Как можно сохранить в памяти то, чего в реальности не существует? Ведь, числа — это просто абстрактные понятия.
Я могу представить себе одно яблоко или один карандаш. Но это будут образы именно яблок или карандашей. А как представить и сохранить в памяти число? Зачастую, мы просто рисуем в своем воображении «картинку» этого числа — определенную цифру.
Если бы я сказал древнему римлянину запомнить число одиннадцать, он бы представил в уме латинскую букву икс с палочкой (XI), а затем вспоминал бы эту картинку каждый раз, когда хотел вспомнить нужное число. Мы же сохраняем этот образ в виде двух палочек с крючками — 11, то есть, также оперируем картинками и образами.
А что делает смартфон с числами 1 и 0? Как он физически их «запоминает»? Прежде, чем мы сможем ответить на этот вопрос, нужно разобраться с более фундаментальным и важным понятием. Об этом и пойдет речь во второй части.
Что такое транзистор и почему в iPhone 12 их около 12 млрд штук?
С устройством транзистора мы подробно разбирались в статье о том, что такое техпроцесс (те самые 7 или 5 нанометров, которые рекламируют производители смартфонов при выпуске очередного процессора).
Вкратце напомню, что транзистор — это крохотный переключатель (или выключатель), который мы можем «открывать» и «закрывать», словно кран с водой.
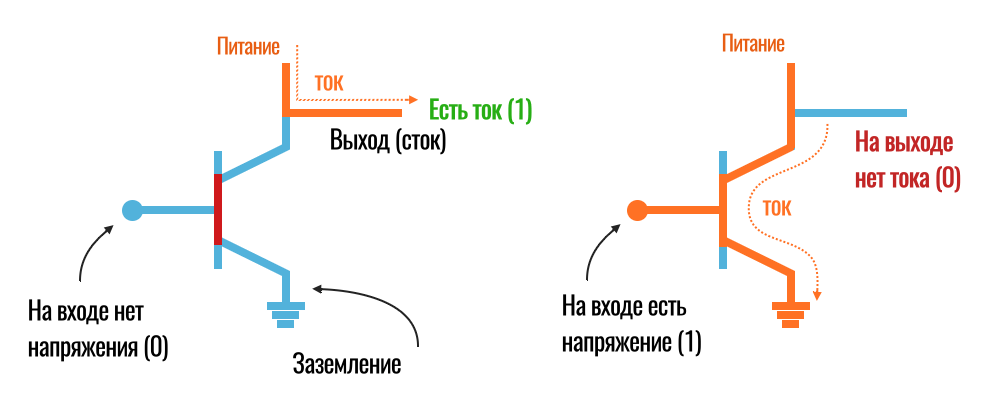
Главная особенность транзистора — это три контакта (электрода), называемые исток, затвор и сток. На исток подается основное напряжение от аккумулятора смартфона. Затвор, как можно догадаться по смыслу — это тот самый «кран», открыв который, ток пойдет на выход (сток), то есть, успешно пройдет через транзистор:
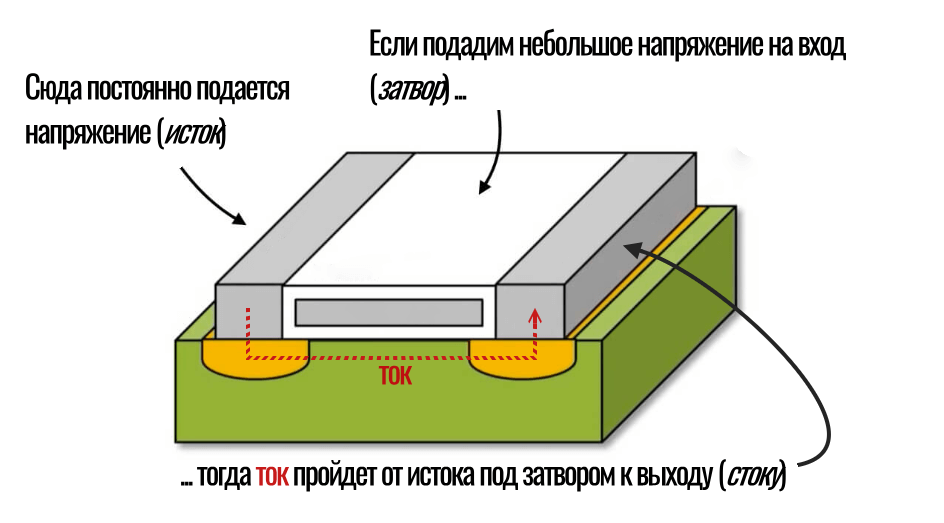
Открывается и закрывается транзистор при помощи небольшого напряжения, подаваемого на затвор. Если напряжение на затворе выше определенного порога, транзистор начинает пропускать ток, в противном случае — нет.
Такое незамысловатое устройство позволяет нам «щелкать» выключателем миллионы раз в секунду. А в одном мобильном процессоре находятся миллиарды транзисторов (например, 11.8 млрд в iPhone 12 или 15.3 млрд в Huawei Mate 40 Pro).
С этим, кажется, всё понятно. Есть маленький транзистор, по которому протекает ток и, в зависимости от состояния затвора, он либо проходит дальше, либо блокируется. Можно отобразить это схематически следующим образом:
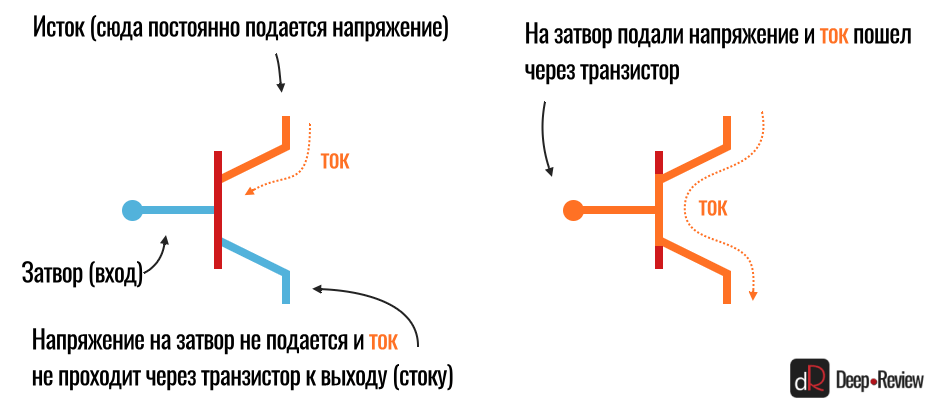
Итак, если мы подаем напряжение на затвор, тогда транзистор открывается и на выходе имеем ток.
Теперь вспоминаем «единицы и нолики». Представим, что напряжение на затворе — это условная «единица», а отсутствие напряжения — это «ноль». Значит, если подать транзистору на вход «единицу» (дать небольшое напряжение на затвор), на выходе мы также получим «единицу», а если подавать «ноль» (отключить напряжение на затворе), то на выходе тоже будет «ноль» (нет тока):
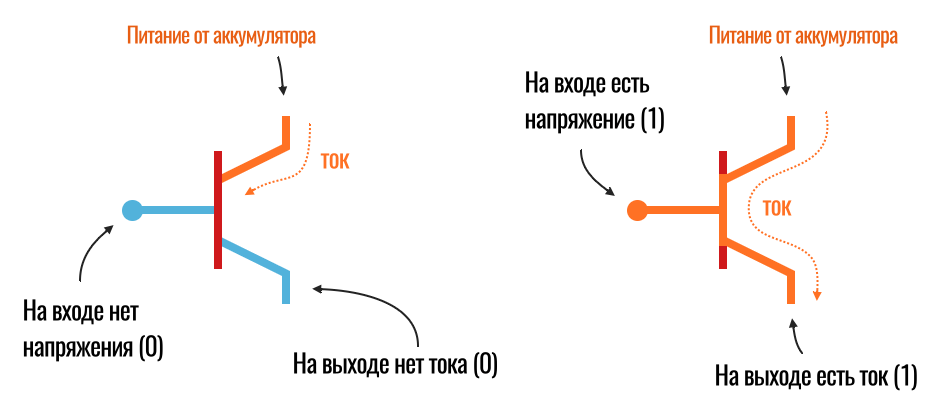
Очень интересное и довольно бесполезное устройство, не находите? Подаем на вход напряжение (единицу) и получаем на выходе напряжение (единицу), не подаем ничего — ничего не получаем. С таким же успехом можно было просто использовать обычный провод.
Но давайте возьмем два транзистора и соединим их так, чтобы получилось два входа и один выход:
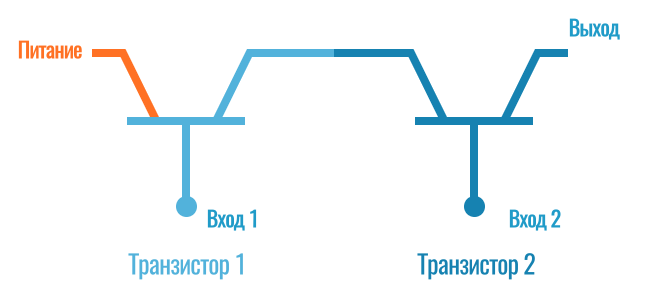
И вот здесь ситуация становится интересней, так как эти два транзистора уже могут умножать числа! В нашем случае (двоичная система счисления, о которой мы говорили в первой части) это 0 и 1:
| Пример | Результат |
| 0*0 | 0 |
| 0*1 | 0 |
| 1*0 | 0 |
| 1*1 | 1 |
Напомню, что на исток транзистора всегда подается ток. В первом примере (0 умножить на 0) мы не будем подавать напряжение на затворы двух транзисторов. Ток зайдет в первый транзистор, «упрется» в закрытый затвор (так как на затворе «0» — нет напряжения) и дальше не пойдет. Соответственно, на выходе из нашей схемы тока не будет (получаем условный «ноль»):
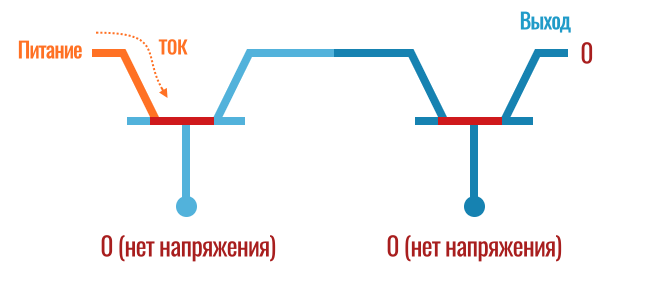
В следующем примере (0 умножить на 1) на вход первого транзистора мы не подаем напряжение, а на второй подаем. В результате из нашего «калькулятора» всё равно не будет выходить ток. Да, второй транзистор «открылся», но к нему не поступает ток от первого транзистора, так как его затвор закрыт:
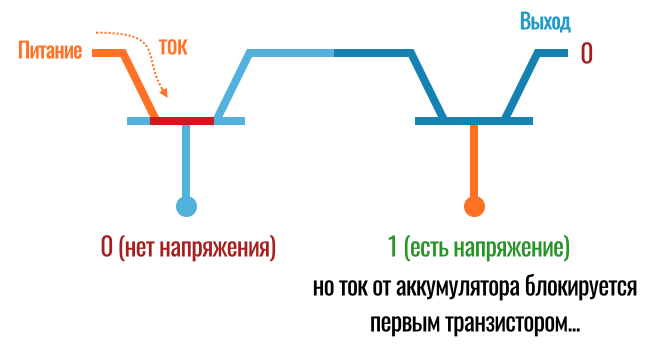
Теперь умножим 1 на 1, то есть, подадим напряжение на входы двух транзисторов. Ток заходит в первый транзистор, проходит через «открытый» затвор, идет на вход ко второму транзистору, а так как и он открыт, то на выходе из всей схемы мы получаем единицу (есть ток):
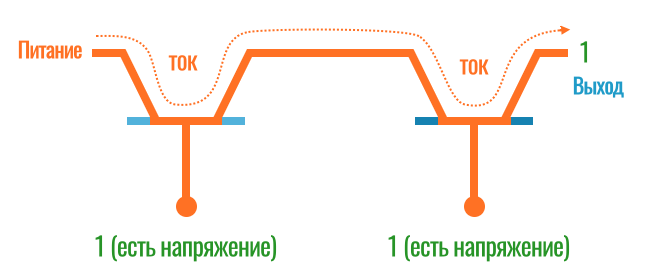
Казалось бы, настолько простая схема, а уже умеет умножать два числа! Такие незамысловатые устройства из нескольких транзисторов называются логическими вентилями (краниками). Конкретно этот вентиль, умножающий два числа, называется И (да, одна буква «и» или на английском AND).
Но почему вентиль называется логическим и почему буква «и»? На самом деле, всё очень просто.
Представьте, что мы не числа умножаем, а проверяем на истинность любые высказывания. Например, я говорю следующие две фразы: «В Африке обитают гепарды» и «Один из африканских гепардов написал эту статью«.
Первое высказывание — это правда (истина). Второе высказывание, очевидно, не является истинной, соответственно, оно ложно. А теперь нам нужно решить простенькую логическую задачку — определить истинность не каждого высказывания по отдельности, а всей фразы целиком: «В Африке обитают гепарды и один из африканских гепардов написал эту статью».
Очевидно, что вся фраза является ложью, так как гепарды не пишут статьи, хотя и обитают в Африке. Получается, если первая часть фразы — истина (1), а вторая — ложь (0), тогда всё высказывание в целом является ложью (0). Если обе части — ложь, то и всё высказывание в целом — ложь.
Если вы посмотрите на картинки выше, то увидите, что наш вентиль AND выдает точно такие же результаты, то есть, он решает простые логические задачки или, другими словами, производит логические операции. Отсюда и название.
Табличку с операциями умножения можно заменить на так называемую таблицу истинности, где вместо чисел у нас два высказывания — либо ложные, либо истинные:
| Выражение | Результат |
| ложь (0) и ложь (0) | ложь (0) |
| ложь (0) и истина (1) | ложь (0) |
| истина (1) и ложь (0) | ложь (0) |
| истина (1) и истина (1) | истина (1) |
А теперь давайте посмотрим на другое высказывание: «Вчера в ресторане я выпил кофе или чай». Если в реальности я пил только кофе, является ли эта фраза истиной? Безусловно! Ведь я не утверждал, что пил кофе и чай.
Получается, мы должны как-то по-другому определять истинность фраз, соединенных союзом ИЛИ. То есть, наш вентиль AND уже работать не будет. Поэтому нам нужно из двух транзисторов создать новое устройство — вентиль ИЛИ (на английском OR).
Сделать это очень легко, достаточно соединить транзисторы не последовательно, как в предыдущем случае, а параллельно:
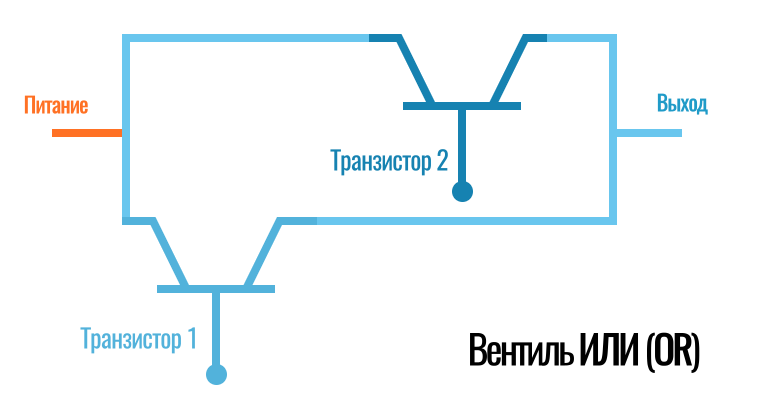
Теперь если мы подаем напряжение (логическую единицу) только на один из транзисторов (на его затвор), на выходе из всего вентиля будет единица (ток):
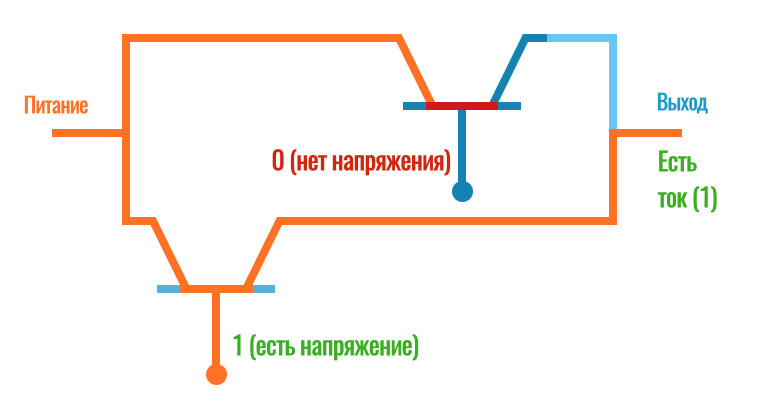
Ложь (0) получится только в том случае, если оба выражения ложны или, другими словами, на выходе из нашего вентиля OR не будет напряжения только в том случае, если не подавать напряжение ни на один из транзисторов. Тогда ток от аккумулятора не пройдет через закрытые затворы:
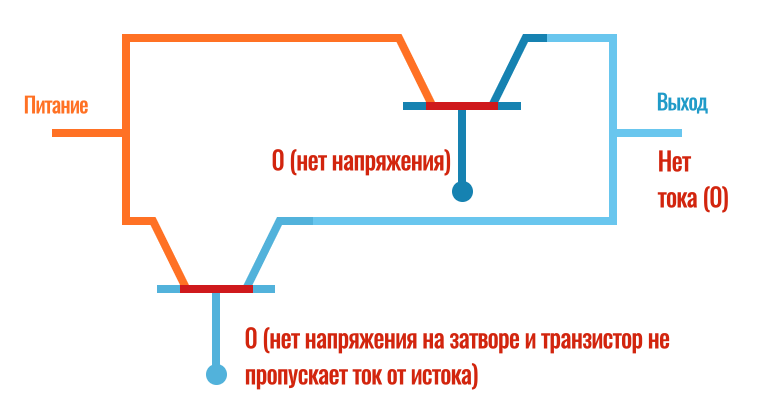
Если присмотреться повнимательней, этот вентиль мог бы уже суммировать два числа. К примеру, подаем на входы 0 и 1, а на выходе получаем 1, значит 0+1=1. Вот еще примеры:
| Пример | Результат |
| 0+0 | 0 |
| 0+1 | 1 |
| 1+0 | 1 |
| 1+1 | 1 |
Проблема возникает только с последним примером, так как 1+1 не может равняться единице. Но в двоичной системе счисления у нас есть только нолики и единички. Что же делать?
Да ровно то же, что мы делаем и в десятичной системе, когда хотим прибавить к девяти еще единицу. Ведь в нашей системе счисления только 10 цифр (от 0 до 9) и мы не можем увеличить 9 еще на 1, так как не существует цифры, которая бы обозначала число десять.
Получается 9+1=0 (начинаем считать заново, с нуля), только теперь слева нужно записать еще единичку, которую мы перенесли в старший разряд:
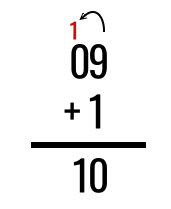
В двоичной системе всё выглядит ровно так же, только мы не можем «подняться выше» единицы, так как есть лишь две цифры — 0 и 1. Соответственно, 1+1 в двоичной системе выглядит, как:
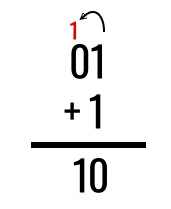
Чтобы решать такие примеры, вентиль OR не подходит, значит, нам нужно создать третий вентиль, который называется исключающее ИЛИ (на английском XOR). Такой вентиль должен работать в точности, как OR, но с одним отличием: когда обе части высказывания истинны, всё высказывание должно быть ложным. Другими словами, когда мы подаем две единицы (подаем на каждый транзистор напряжение), на выходе из вентиля должен быть ноль (отсутствие напряжения).
В обычной жизни мы оперируем именно таким исключающим или союзом, то есть, истинность одной части фразы подразумевает ложность другой, например: «Мне принесли чашку кофе или мне принесли чашку чая». Если мне принесли кофе, значит, это не чай. И наоборот. Если же мы утверждаем, что оба высказывания истинны, значит, вся фраза — ложь, так как одна ее часть исключает другую.
Чтобы реализовать вентиль XOR, вначале нужно сделать еще один вентиль под названием НЕ (на английском — NOT). Всё, что он должен делать — это «переворачивать» значение, которое мы подаем на вход. Если на затвор транзистора подать напряжение, на выходе не должно быть тока. И наоборот, если на входе «ноль» (отсутствует напряжение), на выходе должна быть единица (ток). Такой вентиль еще называется инвертором.
Сделать вентиль NOT очень легко, достаточно его выход расположить сверху (возле истока), а нижний контакт заземлить. Теперь, когда затвор будет закрыт (подаем «ноль» на вход), ток будет спокойно проходить сразу от истока на выход из вентиля. А если открываем затвор, то ток устремится по пути наименьшего сопротивления и уйдет «в землю», а на выходе ничего не будет (0):
Итак, на текущий момент, имея в своем распоряжении только транзисторы и аккумулятор смартфона, который питает их электричеством, мы уже смогли создать три крошечных устройства: вентиль AND, вентиль OR и вентиль NOT:

Надеюсь, пока всё понятно.
Мы уже начинаем видеть какие-то зачатки «логики» и при этом хорошо понимаем физику процесса, но до ответов на все вопросы еще далеко. Я показываю всё на самом низком уровне (на уровне тока) для того, чтобы в работе смартфона и его «мозга» (процессора) не оставалось никакой «магии». Так что наберитесь еще немножко терпения, чтобы узнать больше.
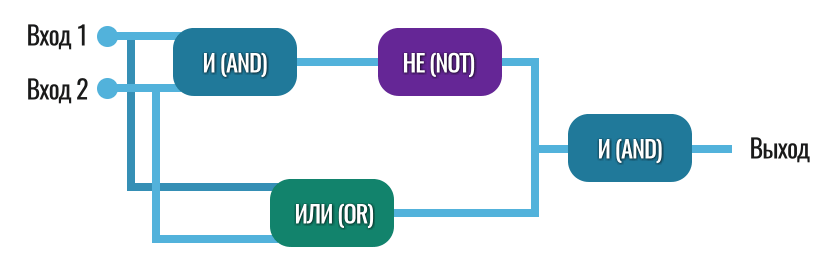
Итак, теперь нужно сделать четвертый вентиль — исключающее ИЛИ (XOR). Он должен выдавать те же результаты, что и OR, за исключением лишь ситуации, когда на оба входа подаются единицы.
Чтобы сделать этот вентиль, мы воспользуемся уже имеющимися — AND, OR и NOT. Для начала параллельно соединим вентили AND и OR, к выходу END подсоединим вентиль NOT, чтобы он инвертировал значение, а затем соединим выходы вентилей NOT и OR со входом еще одного вентиля AND.
Да, звучит всё сложно и запутанно, на теперь посмотрите на картинку и всё станет сразу понятно:
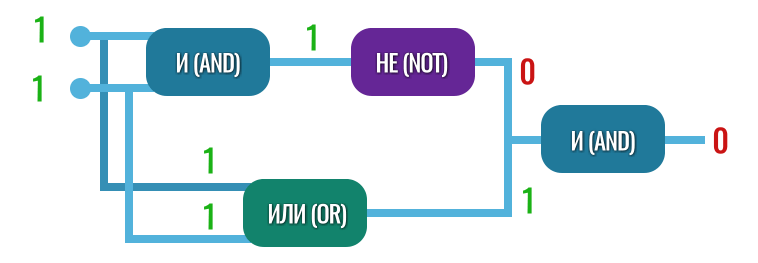
Теперь проверим, как такой вентиль будет работать и подадим на входы две единицы. Вентиль OR в этом случае давал на выходе также единицу, но наш новый вентиль XOR выдаст ноль:
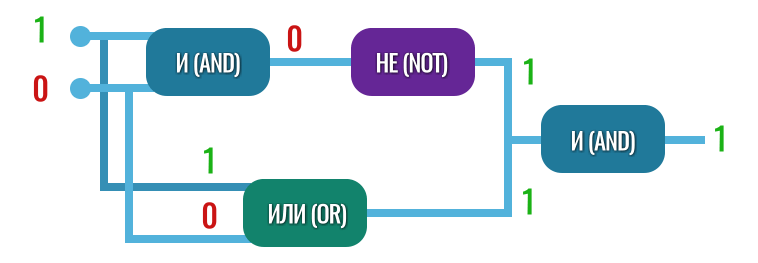
А вот что будет, если подать, к примеру, единицу и ноль:
Или два нуля:
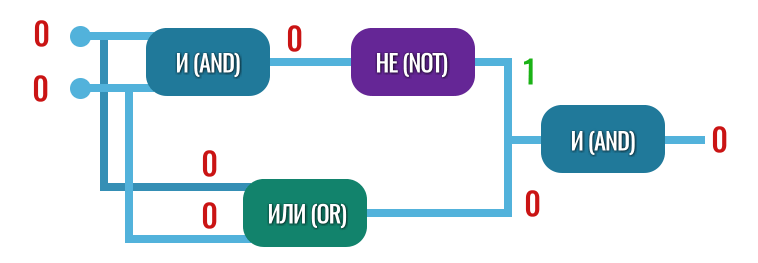
Всё работает! На создание вентиля XOR ушло 7 транзисторов. Как видите, мы уже работали не с отдельными транзисторами, а использовали готовые вентили. Теперь у нас появился еще один сложный вентиль XOR, который дальше мы будем использовать в еще более сложных схемах.
На этом, в принципе, можно было бы и остановиться, так как уже должно приходить понимание того, как из простых выключателей (транзисторов) можно создавать элементарные устройства, которые объединяются в более сложные, а те — в еще более сложные. И так до тех пор, пока мы не построим процессор, состоящий из миллиардов транзисторов. Для этого и нужно такое большое количество этих крохотных выключателей.
Но давайте попробуем создать еще более сложное устройство!
Создаем из транзисторов примитивный калькулятор
В процессе ежедневной работы смартфон производит триллионы операций, складывая, вычитая и умножая различные числа.
Если мы хотим сделать фотографию более яркой, смартфон берет значение яркости каждой точки снимка и прибавляет к нему определенное число, то есть, проделывает операцию сложения для нескольких миллионов точек. Триллионы вычислений также происходят во время игр, просмотра видео или прослушивания музыки.
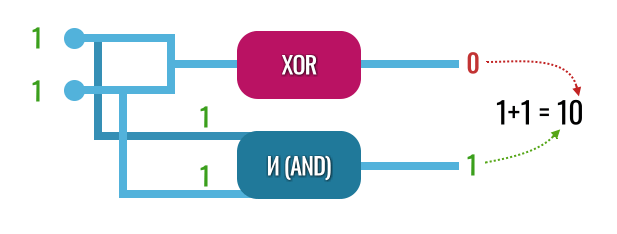
В общем, процессор то и дело постоянно производит математические операции. Но наши элементарные вентили не могут даже сложить два числа. Да, у нас есть вентиль XOR, который работает, как сложение, но если мы подадим на него две единицы, то на выходе получим просто 0, так как единичку нужно перенести в следующий разряд, а он этого делать не умеет.
Давайте исправим этот недостаток.
В двоичной системе 1 + 1 = 10. А это уже два бита (напомню, один бит — это либо единица, либо ноль, т.е. одно число). Наш вентиль XOR при поступлении на вход двух единиц (1+1) выдает только 0.
Чтобы всё работало корректно, мы подключаем к вентилю XOR еще один — AND. Получится вот так:
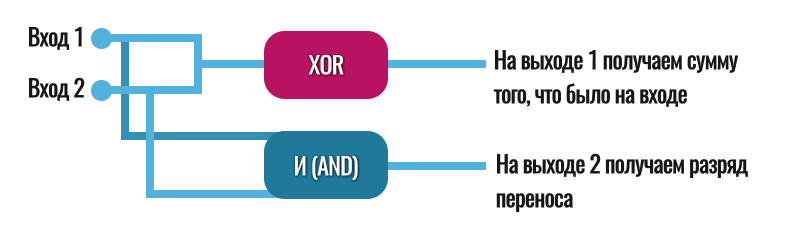
Теперь когда на XOR приходят две единицы, он выдает 0, но две единицы параллельно приходят и на вентиль AND, а тот, как мы разобрались выше, в этом случае выдаст 1. Вот и получаем нужный результат:
Чтобы убедиться, что всё работает, проверим наше новое устройство, отправив на него 1 и 0 (1+0 должно равняться просто 1):
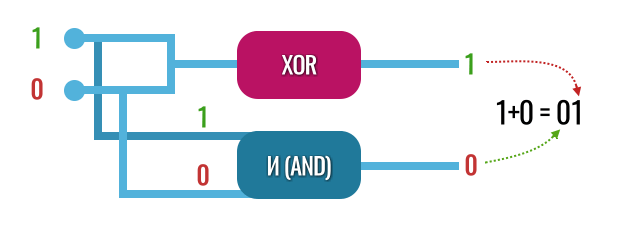
Так и есть! Когда 1 и 0 поступили на вентиль XOR, он выдал единицу, а вентиль AND в этом же случае выдает 0.
Вот так просто у нас получилось новое устройство под названием полусумматор! И теперь мы можем использовать его уже в более сложных схемах, создавая всё более сложные устройства.
К сожалению, толку от этого полусумматора не так много. Наше крохотное устройство из 9 транзисторов может только складывать два бита, то есть, максимум посчитать, сколько будет «один плюс один».
Думаю, вы уже догадались, что можно из двух полусумматоров собрать один полный сумматор и он уже будет работать с тремя битами (складывать два числа одного разряда с учетом переноса из предыдущего разряда). Для этого нам потребуются два полусумматора и один вентиль OR. Но чтобы не перегружать статью лишней информацией, я уже не буду подробно описывать его работу.
Естественно, можно пойти дальше и собрать уже из сумматоров более сложные компоненты, скажем, 8-битный сумматор, который сможет складывать 8-битные числа (вплоть до 256+256). Это потребует сотни транзисторов, но какая разница, если мы можем в крохотном процессоре смартфона разместить 10-15 миллиардов транзисторов?
Процессор смартфона состоит из множества других логических схем для самых разнообразных операций (сложение, вычитание, увеличение или уменьшение числа на единицу, перевод чисел из положительных в отрицательные и наоборот, умножение и пр.).
Если раньше мы складывали транзисторы в вентили, а затем из вентилей создавали более сложные устройства (например, полусумматоры), то теперь нужно собрать всё воедино, создав тем самым АЛУ (арифметико-логическое устройство) — блок процессора, отвечающий за выполнение всех арифметических и логических операций:
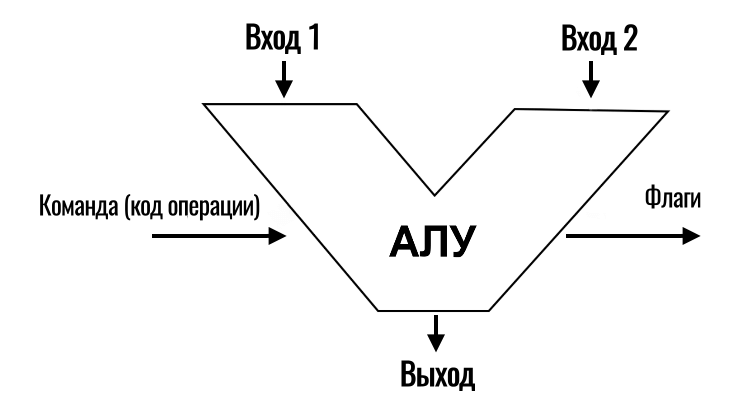
На входы в этот блок мы подаем данные, над которыми нужно проделать определенные операции. Сам код операции (что именно нужно сделать) мы также подаем на еще один вход в АЛУ. Например, 0101 — это код сложения, а 0011 — означает, что нужно произвести вычитание.
Естественно, из АЛУ есть выход, куда отправляется готовый результат. Также из АЛУ выходят различные флаги (признаки), например, есть флаг отрицательного числа, если он равняется единице, то мы знаем, что число — отрицательное.
К сожалению, несмотря на объем статьи, она до сих пор не отвечает на многие вопросы. Всё еще не понятно, как именно числа хранятся в памяти, кто или что указывает процессору, какие конкретно операции и в какой последовательности нужно делать. Да и как, собственно, эти «указания» выглядят?
Со всем этим мы разберемся в следующей части, которая должна сложить все пазлы в единую понятную картину.
Алексей, главный редактор Deep-Review
P.S. Не забудьте подписаться в Telegram на наш научно-популярный сайт о мобильных технологиях, чтобы не пропустить самое интересное!
